设数列{an}的前n项和为Sn.已知a1=a,an+1=2Sn-2n,n∈N*.
(Ⅰ)设bn=Sn-2n,求数列{bn}的通项公式;
(Ⅱ)若an+1≤an,n∈N*,求a的取值范围.
解:(Ⅰ)依题意,S
n+1-S
n=a
n+1=2S
n-2
n,
即S
n+1=3S
n-2
n,
由此得S
n+1-2
n+1=3(S
n-2
n).
即b
n+1=3b
n(4分)
因此,所求通项公式为:
b
n=S
n-2
n=(S
1-2)•3
n-1=(a-2)•3
n-1,n∈N
*.①(6分)
(Ⅱ)由①知S
n=(a-2)3
n-1+2
n,n∈N
*,
于是,当n≥2时,
a
n=S
n-S
n-1=(a-2)3
n-1+2
n-[(a-2)3
n-2+2
n-1]
=2(a-2)3
n-2+2
n-1,
∴a
n+1-a
n=2(a-2)3
n-1+2
n-[2(a-2)3
n-2+2
n-1]
=4(a-2)3
n-2+2
n-1
=
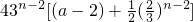
.(8分)
当n≥2时,a
n+1≤a
n
?
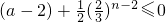
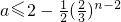

(10分)
又n=1时,a
2≤a
1?2a-2≤a
?a≤2(11分)
所以?n∈N
*,a的取值范围是
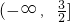
(12分)
分析:(Ⅰ)依题意,S
n+1=3S
n-2
n,所以b
n+1=3b
n,由此能求出数列{b
n}的通项公式.
(Ⅱ)由S
n=(a-2)3
n-1+2
n,n∈N
*,知当n≥2时,a
n=2(a-2)3
n-2+2
n-1,a
n+1-a
n=
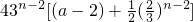
.n≥2时,a
n+1≤a
n?
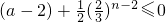
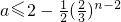

;n=1时,a
2≤a
1?2a-2≤a?a≤2,由此能求出a的取值范围.
点评:本题考查数列的通项公式的求法和求实数a的取值范围,解题时要认真审题,仔细解答,注意数列递推式的灵活运用.

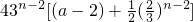 .(8分)
.(8分)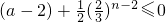
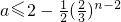
 (10分)
(10分)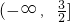 (12分)
(12分)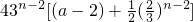 .n≥2时,an+1≤an?
.n≥2时,an+1≤an?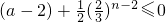
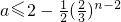
 ;n=1时,a2≤a1?2a-2≤a?a≤2,由此能求出a的取值范围.
;n=1时,a2≤a1?2a-2≤a?a≤2,由此能求出a的取值范围.
