Question

15．海轮“和谐号”从A处以每小时21海里的速度出发，海轮“奋斗号”在A处北偏东45°的方向，且与A相距10海里的C处，沿北偏东105°的方向以每小时9海里的速度行驶，则海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为$\frac{2}{3}$小时．

Answer 1

分析 设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x小时，由已知得△ABC中，AC=10，AB=21x，BC=9x，∠ACB=120°，由此利用余弦定理能求出结果．

解答 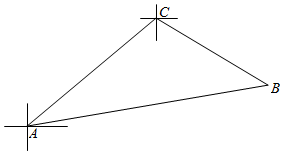解设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x小时，
如图，则由已知得△ABC中，AC=10，AB=21x，BC=9x，∠ACB=120°，
由余弦定理得：（21x）²=100+（9x）²-2×10×9x×cos120°，
整理，得36x²-9x-10=0，
解得x=$\frac{2}{3}$或x=-$\frac{5}{12}$（舍）．
∴海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为$\frac{2}{3}$小时．
故答案为：$\frac{2}{3}$．

点评 本题考查解三角形在生产生活中的实际运用，是中档题，解题时要认真审题，作出图形，利用余弦定理求解．