
| ���� | 7��15�� | 8��15�� | 9��15�� | 10��15�� | 11��15�� | 12��15�� |
| �����¶�x���棩 | 36 | 35 | 30 | 24 | 18 | 8 |
| ���ϱ���y | 27 | 29 | 24 | 18 | 15 | 5 |
���� ��1�������оٷ���������¼������������Ӧ�ĸ���ֵ��
��2���������ݼ����$\overline{x}$��$\overline{y}$��$\stackrel{��}{b}$��$\stackrel{��}{a}$������д�����Իع鷽�̣�
��� �⣺��1����������������ѡȡ2�飬����15�ֵȿ���������ֱ�Ϊ
��7��8������7��9������7��10������7��11������7��12����
��8��9������8��10������8��11������8��12����
��9��10������9��11������9��12����
��10��11������10��12������11��12����
����ѡȡ2������ǡ����������������5��������ֱ�Ϊ
��7��8������8��9������9��10������10��11������11��12����
��ѡȡ2������ǡ�������������µĸ���Ϊ$\frac{5}{15}$=$\frac{1}{3}$��
��2������$\overline{x}$=$\frac{1}{4}$����26+30+24+18��=27��
$\overline{y}$=$\frac{1}{4}$����27+24+18+15��=21��
����$\stackrel{��}{b}$=$\frac{��26-27����27-21��+��+��18-27����15-21��}{{��26-27��}^{2}+��{+��18-21��}^{2}}$��0.7��
$\stackrel{��}{a}$=21-0.7��27=2.1��
����y����x�����Իع鷽��Ϊ$\stackrel{��}{y}$=0.7x+2.1��
���� ���⿼�������оٷ���ŵ���͵ĸ������⣬Ҳ�����������Իع鷽�̵����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ���½�������и߶���ѧ�ڷְ����ѧ�������Ծ��������棩 ���ͣ�ѡ����
��֪��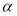 �ձ��뵥λԲ
�ձ��뵥λԲ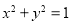 �Ľ���Ϊ
�Ľ���Ϊ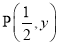 ����
����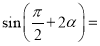 �� ��
�� ��
A�� B��
B��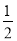 C��
C��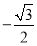 D��
D��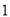
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{\frac{4}{3}��2}]$ | B�� | $��{-�ޣ�0}���ȣ�{\frac{4}{3}��+��}��$ | C�� | ��-�ޣ�0�� | D�� | $��{-�ޣ�0}���ȣ�{\frac{4}{3}��2}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com