设点P是双曲线$\frac{x^2}{4}-{y^2}=1$上的点.F1.F2是其焦点.且∠F1PF2=90°.则△F1PF2的面积是( )A．4B．5C．1D．2 题目和参考答案——青夏教育精英家教网—

4．设点P是双曲线$\frac{x^2}{4}-{y^2}=1$上的点，F₁，F₂是其焦点，且∠F₁PF₂=90°，则△F₁PF₂的面积是（　　）

A．

B．

C．

D．

分析由条件可得||PF₁|-|PF₂||=2a，由题意可知△F₁PF₂为直角三角形利用勾股定理，结合双曲线的定义，即可求出△PF₁F₂的面积．

解答解：由条件可得||PF₁|-|PF₂||=4，由题意可知△F₁PF₂为直角三角形，
设双曲线的焦距为2$\sqrt{5}$，则|PF₁|²+|PF₂|²=|F₁F₂|²=20，b²=1，
故（|PF₁|-|PF₂|）²+2|PF₁|•|PF₂|=|F₁F₂|²=20，即16+2|PF₁|•|PF₂|=20，
故|PF₁|•|PF₂|=2，
故△PF₁F₂的面积为$\frac{1}{2}$|PF₁|•|PF₂|=1．
故选：C．

点评本题考查双曲线的定义与性质，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．

练习册系列答案

68所名校图书小学毕业升学必备系列答案

天利38套新课标全国中考试题精选系列答案

中考试题研究满分特训方案系列答案

中考总复习名师A计划系列答案

百题大过关系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2016-2017学年新疆库尔勒市高二上学期分班考试数学（理）试卷（解析版） 题型：选择题

函数的定义域是（）

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

17．求下列极限：
（1）$\underset{lim}{x→1}$$\sqrt{{x}^{2}+2}$；
（2）$\underset{lim}{x→\frac{π}{4}}$（sinx-cosx）；
（3）$\underset{lim}{x→1}$cos lnx；
（4）$\underset{lim}{x→0}$e^sinx．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．在数列{a_n}中，a₁=1，a₂=2，其前n项和为S_n，且{S_n}成等比数列，则a₅=54．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．有一名同学家开了一个小卖部，他为了研究气温对某种引领销售的影响，记录了2015年7月至12月每月15号下午14时的气温和当天卖出的饮料杯数，得到如下资料：

日期	7月15日	8月15日	9月15日	10月15日	11月15日	12月15日
摄氏温度x（℃）	36	35	30	24	18	8
饮料杯数y	27	29	24	18	15	5

该同学确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选中的2组数据进行检验．
（1）求选取2组数据恰好是相邻的两个月的概率；
（2）若选中的是8月与12月的两组数据，根据剩下的4组数据，求出y关于x的线性回归方程$\hat y=bx+\hat a$．
附：对于一组数据（x₁，y₁），（x₂，y₂），…，（x_n，y_n），其回归直线$\hat a=\overline y-\hat b\overline x$的斜率和截距的最小二乘估计分别为：$b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．

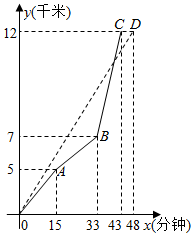如图，在一次自行车越野赛中，甲，乙两名选手所走的路程y（千米）随时间x（分钟）变化的图象（全程）分别用实线（O→A→B→C）与虚线（ OD）表示，那么，在本次比赛过程中，乙领先甲时的x的取值范围是0＜x＜38．