练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．已知等比数列{an}为递增数列，其前n项和为Sn，若a3=8，S3=${∫}_{0}^{2}$（4x+3）dx，则公比q=2．

    分析 求定积分S3=${∫}_{0}^{2}$（4x+3）dx=14，从而可得8（1+$\frac{1}{q}$+$\frac{1}{{q}^{2}}$）=14，从而解得．

    解答 解：S3=${∫}_{0}^{2}$（4x+3）dx=2x2+3x|${\;}_{0}^{2}$=8+6=14，
    则S3=a3（1+$\frac{1}{q}$+$\frac{1}{{q}^{2}}$）=14，
    解得，q=2，
    故答案为：2．

    点评 本题考查了定积分的求法及等比数列的性质的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．直线y=k（x+1）（k∈R）与不等式组$\left\{\begin{array}{l}2x+y-2≤0\\ 2x-y-2≤0\\ x≥0\end{array}\right.$?，表示的平面区域有公共点，则k的取值范围是（　　）
    A．[-2，2]B．（-∞，-2]∪[2，+∞）C．[-$\frac{1}{2}$，$\frac{1}{2}$]D．（-∞，-$\frac{1}{2}$]∪[$\frac{1}{2}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设点P是双曲线$\frac{x^2}{4}-{y^2}=1$上的点，F1，F2是其焦点，且∠F1PF2=90°，则△F1PF2的面积是（　　）
    A．4B．5C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．某工厂对一批共50件的机器零件进行分类检测，其重量（克）统计如下：
    重量段[80，85）[85，90）[90，95）[95，100）
    件数5m12n
    规定重量在82克及以下的为甲型，重量在85克及以上的为乙型，已知该批零件有甲型2件．
    （1）从该批零件中任选1件，若选出的零件重量在[95，100]内的概率为0.26，求m的值；
    （2）从重量在[80，85）的5件零件中，任选2件，求其中恰有1件为甲型的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知函数y=f（x）+x3为偶函数，且f（10）=10，若函数g（x）=f（x）+6，则g（-10）=2016．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．某工厂师徒二人加工相同型号的零件，是否加工出精品互不影响．已知师傅加工一个零件是精品的概率为$\frac{2}{3}$，徒弟加工一个零件是精品的概率为$\frac{1}{2}$，师徒二人各加工2个零件不全是精品的概率为（　　）
    A．$\frac{8}{9}$B．$\frac{2}{3}$C．$\frac{1}{3}$D．$\frac{1}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

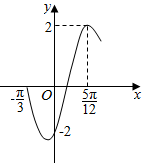    4．函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则ω，φ的值分别是（　　）
    A．$2\;，\;-\frac{π}{3}$B．$2\;，\;-\frac{π}{6}$C．$4\;，\;-\frac{π}{6}$D．$4\;，\;\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．某银行在我市举行了“网上银行、手机银行办理业务免费政策”满意度测评，共有10000人参加了这次测评（满分100分，得分全为整数），为了解本次测评分数情况，从中随机抽取了部分人的测评分数进行统计，整理见如表：
    组别 分组 频数  频率
     1[50，60）a 0.08 
     2[60，70）15 0.3 
     3[70，80）21c 
     4[80，90）6 0.12 
     5[90，100）40.08 
    合计 b 1.00 
    （1）求出表中a，b，c的值；
    （2）若分数字80（含80分）以上表示对“网上银行、手机银行办理业务免费政策”非常满意，其中分数在90（含有90分）以上表示“十分满意”，现从被抽取的“”非常满意人群中随机抽取2人，求至少一人分数是“十分满意”的概率；
    （3）请你根据样本数据估计全市的平均测评分数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，则符合条件$|\begin{array}{l}{z}&{1+i}\\{2}&{1}\end{array}|$=0的复数z对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    同步练习册答案