
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
分析 师徒二人各加工2个零件不全是精品的对立事件是师徒二人各加工2个零件全是精品,由此利用对立事件概率计算公式能求出结果.
解答 解:∵师傅加工一个零件是精品的概率为$\frac{2}{3}$,徒弟加工一个零件是精品的概率为$\frac{1}{2}$,
师徒二人各加工2个零件不全是精品的对立事件是师徒二人各加工2个零件全是精品,
∴师徒二人各加工2个零件不全是精品的概率:
p=1-${C}_{2}^{2}(\frac{2}{3})^{2}{C}_{2}^{2}(\frac{1}{2})^{2}$=$\frac{8}{9}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
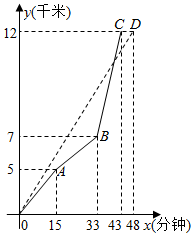 如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.
如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2+3+…+2k+2(k+1)=2k2+k+2(k+1)2+(k+1) | |
| B. | 1+2+3+…+2k+2(k+1)=2(k+1)2+(k+1) | |
| C. | 1+2+3+…+2k+2k+1+2(k+1)=2k2+k+2(k+1)2+(k+1) | |
| D. | 1+2+3+…+2k+2k+1+2(k+1)=2(k+1)2+(k+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | C第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com