
分析 设正系数5次多项式f(x)=ax5+bx4+cx3+dx2+ex+f,则由两个条件求得f(x)=ax5+bx4+7ax3+bx2+ax,可得$\frac{f(3)}{f(2)}$=$\frac{18t+87}{4t+18}$=$\frac{9(2t+9)+6}{2•(2t+9)}$=$\frac{9}{2}$+$\frac{3}{2t+9}$,再利用t>0以及不等式的性质求得它的范围.
解答 解:设正系数5次多项式f(x)=ax5+bx4+cx3+dx2+ex+f,其中a、b、c、d、e、f>0.
则由f(x)=x6f($\frac{1}{x}$),可得 ax5+bx4+cx3+dx2+ex+f=x6•(a${(\frac{1}{x})}^{5}$+b${(\frac{1}{x})}^{4}$+c${(\frac{1}{x})}^{3}$+d${(\frac{1}{x})}^{2}$+e$\frac{1}{x}$+f)
=ax+bx2+cx3+dx4+ex5+fx6,
∴f=0,a=e,b=d,故 f(x)=ax5+bx4+cx3+bx2+ax.
再根据f(2)=10f(1),可得32a+16b+8c+4b+2a=10(a+b+c+b+a),
求得c=7a,故f(x)=ax5+bx4+7ax3+bx2+ax,
∵$\frac{f(3)}{f(2)}$=$\frac{435a+90b}{90a+20b}$=$\frac{435+90•\frac{b}{a}}{90+20•\frac{b}{a}}$=$\frac{87+18•\frac{b}{a}}{18+4•\frac{b}{a}}$,$\frac{b}{a}$>0,设t=$\frac{b}{a}$>0,
则$\frac{f(3)}{f(2)}$=$\frac{18t+87}{4t+18}$=$\frac{9(2t+9)+6}{2(2t+9)}$=$\frac{9}{2}$+$\frac{3}{2t+9}$∈($\frac{9}{2}$,$\frac{29}{6}$).
点评 本题主要考查二项式定理,函数与不等式的性质应用,转化是解题的关键和难点,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
已知数列{an}满足a1=1,|an+1-an|=pn,n∈N*.
(1)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;
(2)若p=,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房号/户型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A户型 | 0.98 | 0.99 | 1.06 | 1.17 | 1.10 | 1.21 | a | 1.09 | 1.14 |
| B户型 | 1.08 | 1.11 | 1.12 | b | 1.26 | 1.27 | 1.26 | 1.25 | 1.28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
已知函数 .
.
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角,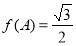 ,
, ,
, ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com