已知数列{an}满足a1＝1.|an+1-an|＝pn.n∈N*.(1)若{an}是递增数列.且a1.2a2.3a3成等差数列.求p的值,(2)若p＝.且{a2n-1}是递增数列.{a2n}是递减数列.求数列{an}的通项公式．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

已知数列{an}满足a1＝1，|an＋1－an|＝pn，n∈N*.

（1）若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；

（2）若p＝，且{a2n－1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2016-2017学年河北省高二8月月考数学试卷（解析版） 题型：解答题

已知直线l经过点（0，－2），其倾斜角为60°.

（1）求直线l的方程；

（2）求直线l与两坐标轴围成三角形的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．2016年1月份，某家电公司为了调查用户对该公司售后服务的满意度，随机调查了10名使用该公司产品的用户，用户通过“10分制”对公司售后服务进行评价．分数不低于9.5分的用户为满意用户，分数低于9分的用户为不满意用户，其它分数的用户为基本满意用户．已知这10名用户的评分分别为：7.6，8.3，8.7，8.9，9.1，9.2，9.3，9.4，9.9，10．
（Ⅰ）从这10名用户的不满意用户和基本满意用户中各抽取一人，求这两名用户评分之和大于18的概率；
（Ⅱ）从这10名用户的满意用户和基本满意用户中任意抽取两人，求这两名用户至少有一人为满意用户的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．△ABC中，角A，B，C对应的边分别为a，b，c，若sinA，sinB，sinC成等差数列，且$tanC=2\sqrt{2}$，则$\frac{sinB}{sinA}$等于（　　）

A．

$\frac{10}{9}$

B．

$\frac{14}{9}$

C．

$\frac{5}{3}$

D．

$\frac{3}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．

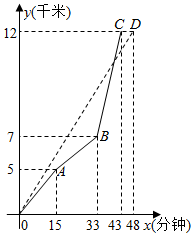如图，在一次自行车越野赛中，甲，乙两名选手所走的路程y（千米）随时间x（分钟）变化的图象（全程）分别用实线（O→A→B→C）与虚线（ OD）表示，那么，在本次比赛过程中，乙领先甲时的x的取值范围是0＜x＜38．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．若函数$f（x）={log_{\frac{1}{3}}}x+\frac{1}{x}+a$的零点在区间（1，+∞）上，则实数a的取值范围是（　　）

A．

（-∞，0）

B．

（-∞，-1）

C．

（-1，+∞）

D．

（0，+∞）

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．在用数学归纳法证明等式1+2+3+…+2n=2n²+n（n∈N^*）的第（ii）步中，假设n=k时原等式成立，那么在n=k+1时需要证明的等式为（　　）

	A．	1+2+3+…+2k+2（k+1）=2k²+k+2（k+1）²+（k+1）
	B．	1+2+3+…+2k+2（k+1）=2（k+1）²+（k+1）
	C．	1+2+3+…+2k+2k+1+2（k+1）=2k²+k+2（k+1）²+（k+1）
	D．	1+2+3+…+2k+2k+1+2（k+1）=2（k+1）²+（k+1）