练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．实数x，y满足条件$\left\{\begin{array}{l}{x+y-4≤0}\\{x-2y+2≥0}\\{x≥0，y≥0}\end{array}\right.$，则z=x-y-1的最小值为-2．

    分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．

    解答 解：由约束条件$\left\{\begin{array}{l}{x+y-4≤0}\\{x-2y+2≥0}\\{x≥0，y≥0}\end{array}\right.$作出可行域如图，

    由z=x-y-1，得y=x-z-1，
    由图可知，当直线y=x-z-1过点A（0，1）时，直线在y轴上的截距最大，z有最小值为0-1-1=-2．
    故答案为：-2．

    点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016-2017学年重庆市高二上学期入学考试数学试卷（解析版） 题型：解答题

    已知函数，

    （1）求不等式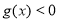的解集；

    （2）若对一切，均有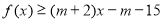成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2016-2017学年河北省高二8月月考数学试卷（解析版） 题型：解答题

    已知四棱锥P－ABCD（图1）的三视图如图2所示，△PBC为正三角形，PA垂直底面ABCD，俯视图是直角梯形

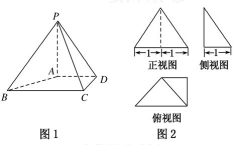
    （1）求正视图的面积；

    （2）求四棱锥P－ABCD的体积；

    （3）求证：AC⊥平面PAB.

    查看答案和解析>>

    科目：高中数学 来源：2016-2017学年河北省高二8月月考数学试卷（解析版） 题型：选择题

    算法S1 m=a

    S2 若b<m，则m=b

    S3 若c<m，则m=d

    S4 若d<m，则 m=d

    S5 输出m，则输出m表示（ ）

    A．a，b，c，d中最大值

    B．a，b，c，d中最小值

    C．将a,b,c,d由小到大排序

    D．将a，b，c，d由大到小排序

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．直线y=k（x+1）（k∈R）与不等式组$\left\{\begin{array}{l}2x+y-2≤0\\ 2x-y-2≤0\\ x≥0\end{array}\right.$?，表示的平面区域有公共点，则k的取值范围是（　　）
    A．[-2，2]B．（-∞，-2]∪[2，+∞）C．[-$\frac{1}{2}$，$\frac{1}{2}$]D．（-∞，-$\frac{1}{2}$]∪[$\frac{1}{2}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜π）经过点（$\frac{π}{12}$，-2），（$\frac{7π}{12}$，2），且在区间（$\frac{π}{12}$，$\frac{7π}{12}$），上为单调函数．
    （Ⅰ）求ω，φ的值；
    （Ⅱ）设an=nf（$\frac{nπ}{3}$）（n∈N*），求数列{an}的前30项和S30．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某电子商务公司随机抽取l 000名网络购物者进行调查．这1000名购物者2015年网上购物金额（单位：万元）均在区间[0.3，0.9]内，样本分组为：[0.3，0.4），[0.4，0.5），[0.5，0.6），[0.6，0.7），[0.7，0.8），[0.8，0.9]．购物金额的频率分布直方图如下：
    电商决定给抽取的购物者发放优惠券；购物金额在[0.3，0.6）内的购物者发放100元的优惠券，购物金额在[0.6，0.9]内的购物者发放200元的优惠券，现采用分层抽样的方式从获得100元和200元优惠券的两类购物者中共抽取10人，再从这10人中随机抽取3人进行回访，求此3人获得优惠券总金额X（单位：元）的分布列和均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知$\overrightarrow m=（sinx，\frac{1}{2}），\overrightarrow n=（cosx，cos（2x+\frac{π}{6}））$，$f（x）=\overrightarrow m•\overrightarrow n+\frac{3}{2}$
    （1）试求函数f（x）的单调递增区间；
    （2）把函数f（x）的横坐标缩小到原来的一半，再向右平移$\frac{π}{6}$个单位，得到函数g（x），在锐角△ABC中，△ABC的三角A，B，C所对的边分别为a，b，c，且$g（B）=\frac{3}{2}$，且$\frac{π}{6}＜B$，b=3，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．某工厂师徒二人加工相同型号的零件，是否加工出精品互不影响．已知师傅加工一个零件是精品的概率为$\frac{2}{3}$，徒弟加工一个零件是精品的概率为$\frac{1}{2}$，师徒二人各加工2个零件不全是精品的概率为（　　）
    A．$\frac{8}{9}$B．$\frac{2}{3}$C．$\frac{1}{3}$D．$\frac{1}{9}$

    查看答案和解析>>

    同步练习册答案