
���� ��1��������������������������ʽ�����Ǻ�ȱ任������f��x���Ľ���ʽ�����������Һ����ĵ����ԣ���ú���f��x���ĵ����������䣮
��2������������y=Asin����x+�գ���ͼ��任�������g��x���Ľ���ʽ�����������Ҷ����Լ���������ʽʽ����á�ABC��������ֵ��
��� �⣺��1����$\overrightarrow m=��sinx��\frac{1}{2}����\overrightarrow n=��cosx��cos��2x+\frac{��}{6}����$��
��$f��x��=\overrightarrow m•\overrightarrow n+\frac{3}{2}=��sinx��\frac{1}{2}��•��cosx��cos��2x+\frac{��}{6}����+\frac{3}{2}=sinxcosx+\frac{1}{2}cos��2x+\frac{��}{6}��+\frac{3}{2}$
=$\frac{1}{2}$sin2x+$\frac{1}{2}$��cos2x•$\frac{\sqrt{3}}{2}$-sin2x•$\frac{1}{2}$��+$\frac{3}{2}$=$\frac{1}{4}$sin2x+$\frac{\sqrt{3}}{4}$cos2x+$\frac{3}{2}$=$\frac{1}{2}$sin��2x+$\frac{��}{3}$��+$\frac{3}{2}$��
��$2k��-\frac{��}{2}��2x+\frac{��}{3}��2k��+\frac{��}{2}$�����$k��-\frac{5��}{12}��x��k��+\frac{��}{12}$��
�ɵ�f��x���ĵ���������Ϊ$[k��-\frac{5��}{12}��k��+\frac{��}{12}]��k��Z$
��2���Ѻ���f��x���ĺ�������С��ԭ����һ�룬�ɵ�y=$\frac{1}{2}$sin��4x+$\frac{��}{3}$��+$\frac{3}{2}$��ͼ��
������ƽ��$\frac{��}{6}$����λ�õ�����$g��x��=\frac{3}{2}+\frac{1}{2}sin��4x-\frac{��}{3}��$��ͼ��
��$g��B��=\frac{3}{2}$����$\frac{3}{2}+\frac{1}{2}sin��4B-\frac{��}{3}��=\frac{3}{2}$��
��$\frac{1}{2}sin��4B-\frac{��}{3}��=0��4B-\frac{��}{3}=k��B=\frac{k��}{4}+\frac{��}{12}��k��z$��
��k=0ʱ��$B=\frac{��}{12}$�������⣻��$k=1��B=\frac{��}{3}$��
�������Ҷ����ɵ�b2=a2+c2-2accosB=a2+c2-ac��ac����ac��9��
${S_{��ABC}}=\frac{1}{2}acsinB��\frac{1}{2}��9��\frac{{\sqrt{3}}}{2}=\frac{{9\sqrt{3}}}{4}$�����ҽ���a=bʱ����ABC��������ֵΪ$\frac{9\sqrt{3}}{4}$��
���� ������Ҫ����������������������ʽ�����Ǻ�ȱ任��y=Asin����x+�գ���ͼ��任���ɣ����Ҷ����Լ���������ʽ��Ӧ�ã������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ���½�������и߶���ѧ�ڷְ����ѧ�������Ծ��������棩 ���ͣ�ѡ����
��֪x��y���� ��
��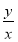 ����ֵ�ǣ� ��
����ֵ�ǣ� ��
A.���ֵ��2����Сֵ��1 B.���ֵ��1����Сֵ��0
C.���ֵ��2����Сֵ��0 D.�����ֵ����Сֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{10}{9}$ | B�� | $\frac{14}{9}$ | C�� | $\frac{5}{3}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
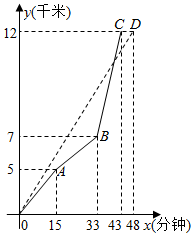 ��ͼ����һ�����г�ԽҰ���У��ף�������ѡ�����ߵ�·��y��ǧ�ף���ʱ��x�����ӣ��仯��ͼ��ȫ�̣��ֱ���ʵ�ߣ�O��A��B��C�������ߣ� OD����ʾ����ô���ڱ��α��������У������ȼ�ʱ��x��ȡֵ��Χ��0��x��38��
��ͼ����һ�����г�ԽҰ���У��ף�������ѡ�����ߵ�·��y��ǧ�ף���ʱ��x�����ӣ��仯��ͼ��ȫ�̣��ֱ���ʵ�ߣ�O��A��B��C�������ߣ� OD����ʾ����ô���ڱ��α��������У������ȼ�ʱ��x��ȡֵ��Χ��0��x��38���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+2+3+��+2k+2��k+1��=2k2+k+2��k+1��2+��k+1�� | |
| B�� | 1+2+3+��+2k+2��k+1��=2��k+1��2+��k+1�� | |
| C�� | 1+2+3+��+2k+2k+1+2��k+1��=2k2+k+2��k+1��2+��k+1�� | |
| D�� | 1+2+3+��+2k+2k+1+2��k+1��=2��k+1��2+��k+1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com