
| A. | 第一象限 | B. | 第二象限 | C. | C第三象限 | D. | 第四象限 |
分析 利用新定义可得关于z的等式,然后利用复数代数形式的乘除运算化简,进一步求得$\overline{z}$得答案.
解答 解:由题意可得:$|\begin{array}{l}{z,}&{1+i}\\{-i,}&{2i}\end{array}|$=z(2i)-(-i)(1+i)=0,
即$z=\frac{1-i}{2i}=\frac{(1-i)(-2i)}{2i(-2i)}=\frac{-2-2i}{4}=-\frac{1}{2}-\frac{i}{2}$,
∴$\overline{z}=-\frac{1}{2}+\frac{i}{2}$,
则复数$\overline{z}$对应的点的坐标为($-\frac{1}{2},\frac{1}{2}$),在第二象限.
故选:B.
点评 本题是新定义题,考查了复数代数形式的乘除运算,是基础题.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
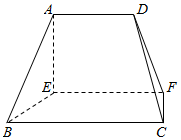 在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6.
在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
已知函数 .
.
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角,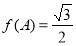 ,
, ,
, ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,求cosA=$\frac{\sqrt{6}}{4}$.
如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,求cosA=$\frac{\sqrt{6}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(-∞,2)内是减函数 | B. | 在(-∞,4)内是减函数 | ||
| C. | 在(-∞,0)内是减函数 | D. | 在(-∞,+∞)内是减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com