
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100) |
| 件数 | 5 | m | 12 | n |
分析 (1)根据题设条件,先求出n的值,进而即可能求出m.
(2)重量在[80,85)的5件零件中,甲型2件,乙型3件,任选2件,先求出基本事件总数,再求出其中恰有1件为甲型包含的基本事件个数,由此能求出恰有1件为甲型的概率.
解答 解:(1)∵从该批零件中任选1件,选出的零件重量在[95,100]内的概率为0.26,
∴n=50×0.26=13,
∴m=50-5-12-13=20.
(2)∵重量在[80,85)的5件零件中,甲型2件,乙型3件,
从重量在[80,85)的5件零件中,任选2件,基本事件总数n=${C}_{5}^{2}$=10,
其中恰有1件为甲型包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6,
∴其中恰有1件为甲型的概率p=$\frac{m}{n}$=0.6.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:选择题
两个球的表面积之差为48π,它们的大圆周长之和为12π,这两个球的半径之差为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
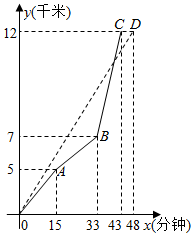 如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.
如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-2,1) | C. | (-$\sqrt{5}$,2) | D. | (-2,$\sqrt{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2+3+…+2k+2(k+1)=2k2+k+2(k+1)2+(k+1) | |
| B. | 1+2+3+…+2k+2(k+1)=2(k+1)2+(k+1) | |
| C. | 1+2+3+…+2k+2k+1+2(k+1)=2k2+k+2(k+1)2+(k+1) | |
| D. | 1+2+3+…+2k+2k+1+2(k+1)=2(k+1)2+(k+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,2) | B. | (1,2) | C. | ($\frac{1}{3}$,2) | D. | (1,$\frac{2}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com