
| A. | ($\sqrt{2}$,$\sqrt{6}$) | B. | ($\sqrt{2}$,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (2,$\sqrt{7}$) |
分析 设直线l:y=kx+m,代入双曲线的方程,设M(x1,y1),N(x2,y2),运用韦达定理和判别式大于0,以及二次的方程有两个大于1的实根,求得k2>$\frac{4}{3}$,运用中点坐标公式,以及直线和圆相切的斜率关系,求得MN的中点P,代入圆的方程可得r的式子,再由不等式的性质,即可得到所求范围.
解答 解:设直线l:y=kx+m,
代入双曲线的方程,可得(1-k2)x2-2kmx-m2-1=0,①
由判别式4k2m2+4(1-k2)(m2+1)>0,
即为m2+1-k2>0,
设M(x1,y1),N(x2,y2),
可得x1+x2=$\frac{2km}{1-{k}^{2}}$,x1x2=$\frac{{m}^{2}+1}{{k}^{2}-1}$>0,
可得k2>1,MN的中点P为($\frac{km}{1-{k}^{2}}$,$\frac{m}{1-{k}^{2}}$),
⊙C:(x-4)2+y2=r2的圆心为(4,0),
由直线与圆相切于P,可得
$\frac{\frac{m}{1-{k}^{2}}}{\frac{mk}{1-{k}^{2}}-4}$=-$\frac{1}{k}$,化为1-k2=$\frac{1}{2}$mk,
即有MN中点坐标为(2,$\frac{2}{k}$),
代入圆的方程可得r2=4+$\frac{4}{{k}^{2}}$>4,
又①有两个大于1的根,则1-k2-2km-m2-1>0,
即为3k2-4>m2≥0,即有k2>$\frac{4}{3}$,
综上可得k2>$\frac{4}{3}$,
即有r2=4+$\frac{4}{{k}^{2}}$<4+3=7,
则有4<r2<7,即2<r<$\sqrt{7}$.
故选:D.
点评 本题考查双曲线的方程和运用,考查直线方程和双曲线的方程联立,运用判别式和韦达定理,以及中点坐标公式,考查直线和圆相切的条件,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年新疆库尔勒市高二上学期分班考试数学(理)试卷(解析版) 题型:解答题
如图,四棱锥 的底面
的底面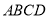 是边长为2的菱形,
是边长为2的菱形,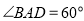 ,已知
,已知 .
.

(1)证明:
(2)若 为
为 的中点,求三棱锥
的中点,求三棱锥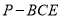 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{3}$,+∞) | B. | [3,+∞) | C. | (3,+∞) | D. | [9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
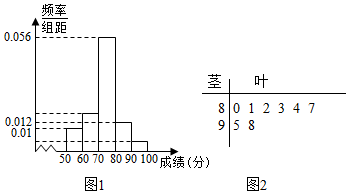
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
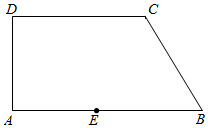 如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)
如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com