
(本题12分)如图所示,直线 ⊥
⊥ 轴,从原点开始向右平行移动到
轴,从原点开始向右平行移动到 处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为
处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为 .
.

(1)求函数 的解析式;
的解析式;
(2)解不等式 .
.
(1) ;(2)
;(2)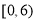 .
.
【解析】
试题分析:(1)根据△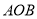 内位于直线
内位于直线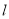 左侧图形的形状分两种情况,分别得出函数
左侧图形的形状分两种情况,分别得出函数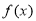 的解析式,并用分段函数表示;在解决函数应用问题时,首先要审清题意,明确自变量及其取值范围,其次要正确列出函数关系式并化简.(2)根据函数
的解析式,并用分段函数表示;在解决函数应用问题时,首先要审清题意,明确自变量及其取值范围,其次要正确列出函数关系式并化简.(2)根据函数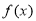 的解析式,分两种情况求解不等式
的解析式,分两种情况求解不等式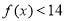 ,并将结果合并.解决这类问题的关键在于合理分类求解,正确合并结果.
,并将结果合并.解决这类问题的关键在于合理分类求解,正确合并结果.
试题解析:(1)由图知,△AOB为等腰直角三角形, 1分
∴当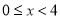 时,
时,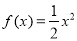 ; 3分
; 3分
当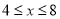 时,
时,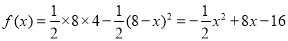 ; 5分
; 5分
∴ 6分
6分
(2)∵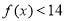 ,∴当
,∴当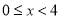 时,显然
时,显然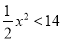 恒成立; 8分
恒成立; 8分
当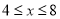 时,有
时,有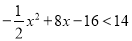 ,即
,即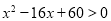 ,解之得
,解之得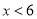 或
或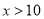 (舍),
(舍),
∴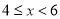 10分
10分
综上,不等式的解集为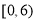 . 12分
. 12分
考点:①利用三角形面积公式,求分段函数解析式;②一元二次不等式的解法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年江西省高一上学期第一次月考数学试卷(解析版) 题型:选择题
幂函数 的图像经过点(2,4),则
的图像经过点(2,4),则 等于( )
等于( )
(A)2 (B)8 (C)16 (D)64
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高一上学期第一次段考数学试卷(解析版) 题型:选择题
设定义域为R的函数 满足
满足 ,且
,且 ,则
,则 的值为( )
的值为( )
A.-1 B.1 C.2014 D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高一上学期第一次段考数学试卷(解析版) 题型:选择题
若集合A、B、C,满足 ,
, ,则A与C之间的关系为( )
,则A与C之间的关系为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省高邮市高二九月月考数学试卷(解析版) 题型:解答题
下面给出的正多边形的边长都是20cm,请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明.
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.



图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com