
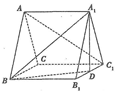
 如图,斜三棱柱ABC-A1B1C1中,AB=AC=2,平面ABC⊥平面B1BCC1,BC=BB1=2$\sqrt{3}$,∠B1BC=60°,D为B1C1的中点.
如图,斜三棱柱ABC-A1B1C1中,AB=AC=2,平面ABC⊥平面B1BCC1,BC=BB1=2$\sqrt{3}$,∠B1BC=60°,D为B1C1的中点.分析 (1)连接AB1交A1B于E,连接DE,有DE∥AC1,根据线面平行的判定即可证明线面平行;
(2)首先证明A1D⊥面B1BCC1,连接DC,利用空间直角坐标系,面B1A1B的法向量与面A1BD的法向量的向量夹角公式求出二面角;
解答 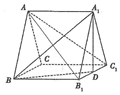 (12分)(1)证明:连接AB1交A1B于E,连接DE,
(12分)(1)证明:连接AB1交A1B于E,连接DE,
由棱柱的性质知ABB1A1为平行四边形,
⇒E为AB1中点,又D为B1C1的中点,
故 $\left.\begin{array}{l}A{C_1}∥DE\\ DE?面{A_1}BD\\ A{C_1}?面{A_1}BD\end{array}\right\}⇒A{C_1}∥面{A_1}BD$;
(2)$\left.\begin{array}{l}面ABC⊥{B_1}BC{C_1}\\ 面ABC∥面{A_1}{B_1}{C_1}\end{array}\right\}⇒面{A_1}{B_1}{C_1}⊥{B_1}BC{C_1}$,
又由题易知A1D⊥B1C1,所以A1D⊥面B1BCC1,
连接DC,可得DB1,DC,DA1两两互相垂直,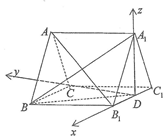
如图,以D为原点,DB1,DC,DA1为x,y,z轴正方向建立空间直角坐标系,
由题易求得:
面B1A1B的法向量$\overrightarrow{n_1}=({\sqrt{3}\;\;,\;\;-1\;\;,\;\;3})$,
面A1BD的法向量$\overrightarrow{n_2}=({\sqrt{3}\;\;,\;\;-2\;\;,\;\;0})$,
所以$cosθ=|{\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}||{\overrightarrow{n_2}}|}}}|=\frac{10}{{\sqrt{13}\sqrt{28}}}=\frac{{5\sqrt{91}}}{91}$.
点评 本题主要考查了线面平行的判断证明,线面垂直的判断证明以及利用向量求解二面角,属中等题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
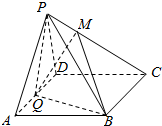 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | ||
| C. | $\frac{1}{8}$ | D. | 以上答案均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2k-1,2k+2](k∈Z) | B. | [2k+1,2k+3](k∈Z) | C. | [4k+1,4k+3](k∈Z) | D. | [4k+2,4k+4](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com