
过已知点(3,0)的直线l与圆x2+y2+x-6y+3=0相交于P,Q两点,且OP⊥OQ(其中O为原点),求直线l的方程.
分析:若设点P(x1,y1),Q(x2,y2),则由OP⊥OQ,可得![]() ·
·![]() =-1.由P,Q分别在圆及直线上,可借助方程,利用根与系数的关系求解.
=-1.由P,Q分别在圆及直线上,可借助方程,利用根与系数的关系求解.
解:设点P(x1,y1),Q(x2,y2),直线l的方程为x+ay-3=0.则点P,Q的坐标分别满足方程组![]()
消去y,得(a2+1)x2+(a2+6a-6)x+3a2-18a+9=0.
所以x1x2=![]() ①
①
消去x,得(a2+1)y2-(7a+6)y+15=0.
所以y1y2=![]() . ②
. ②
因为OP⊥OQ,所以![]() ·
·![]() =-1,
=-1,
即y1y2+x1x2=0.
将①②代入上式,解得a=2,或a=4.
所以直线l的方程为x+2y-3=0,或x+4y-3=0.
点评:本题巧用根与系数的关系,列出y1y2+x1x2=0,进而求方程得解.另外,将过点(3,0)的直线的方程设为x+ay-3=0可避免分类讨论.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| RM |
| RN |
查看答案和解析>>
科目:高中数学 来源: 题型:
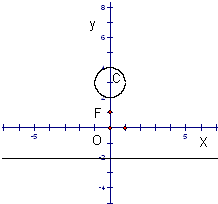 如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.
如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| x2 |
| 4 |
| 1 |
| 2 |
| x2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 5 |
| AM |
| AB |
| AN |
| AC |
| 1 |
| x |
| 1 |
| y |
| ∫ | π 0 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com