
分析 (1)根据等差数列和等比数列的性质即可求出数列{an}的通项公式,
(2)先化简bn,再分别根据等比数列和等差数列的前n项和公式和放缩法即可求出n的最小值.
解答 解:(1)设等比数列{an}的公比为q,依题意:有2a1+a1q2=3a1q,
解得q=1或q=2,
∵a3+2是a2,a4的等差中项,
∴2a3+4=a2+a4,
即2a1q2+4=a1q+a1q3,
当q=1时,不成立,
当q=2时,a1=2,
∴an=2n,
(2)bn=$\frac{1}{{a}_{n}}$+log2$\frac{1}{{a}_{n}}$=$\frac{1}{{2}^{n}}$-n,
∴Sn=b1+b2+…+bn=($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$)-(1+2+3+…+n)=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n(n+1)}{2}$=1-$\frac{1}{{2}^{n}}$-$\frac{n(n+1)}{2}$
∵Sn+35<0,
∴1-$\frac{1}{{2}^{n}}$-$\frac{n(n+1)}{2}$+35<0,
∴$\frac{1}{{2}^{n}}$+$\frac{n(n+1)}{2}$>36恒成立,
∴$\frac{n(n+1)}{2}$≥36恒成立,
∴n(n+1)≥72,
解得n≥8,
∴使Sn+35<0成立的n的最小值是8.
点评 本题考查了等比数列和等差的数列的性质以及前n项和公式以及数列和不等式的关系,属于中档题.


科目:高中数学 来源: 题型:填空题
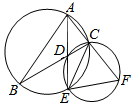 如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.
如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∨q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
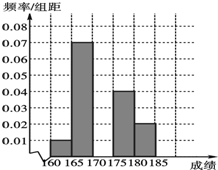 北京某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
北京某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | n | 0.350 |
| 第3组 | [170,175) | 30 | p |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com