
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是相等函数.
解答 解:对于(1),函数g(x)=($\sqrt{x}$)2=x(x≥0),与函数f(x)=|x|(x∈R)的定义域不同,不是相等函数;
对于(2),函数g(x)=$\sqrt{{x}^{2}}$=|x|(x∈R),与函数f(x)=|x|(x∈R)的定义域相同,对应关系也相同,是相等函数;
对于(3),函数s(x)=x(x∈R),与函数f(x)=|x|(x∈R)的对应关系不相同,不是相等函数;
对于(4),函数y=$\left\{\begin{array}{l}{x,x≥0}\\{-x,x<0}\end{array}\right.$=|x|(x∈R),与函数f(x)=|x|(x∈R)的定义域相同,对应关系也相同,是相等函数;
综上,相等的函数是(2)(4).
故答案为:(2)(4).
点评 本题考查了判断两个函数是相等函数的应用问题,是基础题目.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
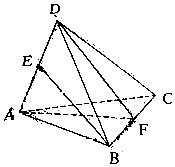 如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.
如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com