
分析 由新定义,可以求出函数的解析式,进而求出x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,实数m的取值范围,及三个实根之间的关系,进而求出x1•x2•x3的取值范围.
解答 解:由2x-1≤x-1,得x≤0,此时f(x)=(2x-1)*(x-1)=-(2x-1)2+2(2x-1)(x-1)-1=-2x,
由2x-1>x-1,得x>0,此时f(x)=(2x-1)*(x-1)=(x-1)2-(2x-1)(x-1)=-x2+x,
∴f(x)=(2x-1)⊕(x-1)=$\left\{\begin{array}{l}{-2x,x≤0}\\{{-x}^{2}+x,x>0}\end{array}\right.$,
作出函数的图象可得,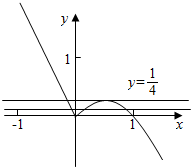
要使方程f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,不妨设x1<x2<x3,
则0<x2<$\frac{1}{2}$<x3<1,且x2和x3,关于x=$\frac{1}{2}$对称,
∴x2+x3=2×$\frac{1}{2}$=1.则x2+x3≥2$\sqrt{{{x}_{2}x}_{3}}$,0<x2x3<$\frac{1}{4}$,等号取不到.
当-2x=$\frac{1}{4}$时,解得x=-$\frac{1}{8}$,
∴-$\frac{1}{8}$<x1<0,
∵0<x2x3<$\frac{1}{4}$,
∴-$\frac{1}{32}$<x1•x2•x3<0,
即x1•x2•x3的取值范围是(-$\frac{1}{32}$,0),
故答案为:(-$\frac{1}{32}$,0).
点评 本题考查根的存在性及根的个数判断,根据已知新定义,求出函数的解析式,并分析出函数图象是解答的关键.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
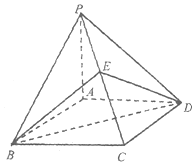 如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com