
分析 (1)利用正交分解可得子弹弹道曲线的参数方程.
(2)①把v0=100m/s,α=$\frac{π}{6}$,t=2代入(1)的参数方程即可得出.
②x=2×100×cos$\frac{π}{6}$,y=h,炮弹的射程S=$\sqrt{{x}^{2}+{y}^{2}}$,代入计算即可得出.
解答 解:(1)子弹弹道曲线的参数方程为$\left\{\begin{array}{l}{x=t{v}_{0}cosα}\\{y=t{v}_{0}sinα-\frac{1}{2}g{t}^{2}}\end{array}\right.$(t为时间).
(2)∵v0=100m/s,α=$\frac{π}{6}$,
∴当t=2时,
①h=2×100sin$\frac{π}{6}$-4.9×22=80.4m.(g=9.8)
②x=2×100×cos$\frac{π}{6}$=100$\sqrt{3}$,y=h,
炮弹的射程S=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{(100\sqrt{3})^{2}+80.{4}^{2}}$≈175.2m.
点评 本题考查了物理斜抛类型的参数方程的应用、位移的正交分解,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=\frac{1}{2}x′}\\{x=y′}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2x′}\\{y=y′}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=4x′}\\{y=y′}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2x′}\\{y=4y′}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
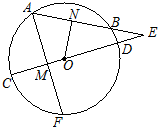 如图,在⊙O中,弦AF交直径CD于点M,弦的延长线交CD的延长线于点E,M、N分别是AF、AB的中点.
如图,在⊙O中,弦AF交直径CD于点M,弦的延长线交CD的延长线于点E,M、N分别是AF、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
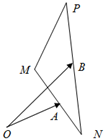 如图,已知$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,且|$\overrightarrow b$|=2|$\overrightarrow a$|=2,任意点M关于点A的对称点为N,点N关于点B的对称点为P,则$\overrightarrow{MP}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)=( )
如图,已知$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,且|$\overrightarrow b$|=2|$\overrightarrow a$|=2,任意点M关于点A的对称点为N,点N关于点B的对称点为P,则$\overrightarrow{MP}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)=( )| A. | 6 | B. | -6 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com