
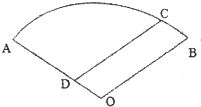
 吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).
吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米). 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
| 产品类别 | A | B | C |
| 产品数量(件) | 1600 | ||
| 样本容量(件) | 160 |
| A、1300 | B、1100 |
| C、130 | D、110 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
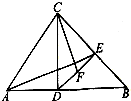 如图,在锐角三角形ABC中,D为C在AB上的射影,E为D在BC上的射影,F为DE上一点,且满足
如图,在锐角三角形ABC中,D为C在AB上的射影,E为D在BC上的射影,F为DE上一点,且满足| EF |
| FD |
| AD |
| DB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sinθ | ||
1+
|
| cosθ |
| 1+tanθ |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com