
| x |
| 2x+y |
| 2y |
| x+2y |
| x |
| 2x+y |
| 2y |
| x+2y |
| 1 | ||
2+
|
2
| ||
1+2
|
| y |
| x |
| 1 |
| 2+t |
| 2t |
| 1+2t |
| 1 |
| t+2 |
| 1 |
| 2t+1 |
| t-1 |
| (t+2)(2t+1) |
| s |
| 2s2+9s+9 |
| 1 | ||
2s+
|
| 9 |
| s |
| 9 |
| s2 |
| 2s2-9 |
| s2 |
2(s2-
| ||
| s2 |
| 9 |
| s |
| 9 |
| s |
| 9 |
| s |
| 1 |
| 2 |
| 1 | ||
2s+
|
| 1 |
| 2 |
| 9 |
| s |
2s•
|
| 2 |
| 1 | ||
2s+
|
| 1 | ||
9+6
|
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| x |
| 2x+y |
| 2y |
| x+2y |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |


科目:高中数学 来源: 题型:
| A、{-3,-2,-1,0} |
| B、(-∞,0) |
| C、(0,+∞) |
| D、{-3,-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:
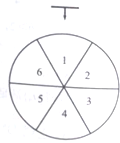 商场销售的某种饮品每件售价36元,成本为20元.对该饮品进行促销;顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针指向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其它情况无奖.
商场销售的某种饮品每件售价36元,成本为20元.对该饮品进行促销;顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针指向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其它情况无奖.| x |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
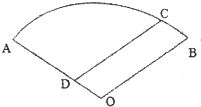 吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).
吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3cosB |
| 1 |
| 3 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com