
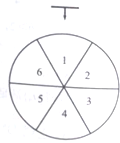
 �̳����۵�ij����Ʒÿ���ۼ�36Ԫ���ɱ�Ϊ20Ԫ���Ը���Ʒ���д������˿�ÿ����һ������������ת��������ͼ��ʾת�̣�ÿ��ֹͣ��ָ��ָ��һ�����֣�������ָ��ͬһ�����֣���һ�Ƚ���������ָ������������ţ�������˳������Ƚ��������������
�̳����۵�ij����Ʒÿ���ۼ�36Ԫ���ɱ�Ϊ20Ԫ���Ը���Ʒ���д������˿�ÿ����һ������������ת��������ͼ��ʾת�̣�ÿ��ֹͣ��ָ��ָ��һ�����֣�������ָ��ͬһ�����֣���һ�Ƚ���������ָ������������ţ�������˳������Ƚ��������������| x |
| 4 |
| x |
| 2 |
| x |
| 2 |
| 6 |
| 63 |
| 1 |
| 36 |
4
| ||
| 63 |
| 4 |
| 36 |
| 5 |
| 36 |
| 5 |
| 36 |
| 335 |
| 1296 |
| x |
| 2 |
| 1 |
| 36 |
| x |
| 2 |
| 4 |
| 36 |
| x |
| 36 |
| 2x |
| 36 |
| x |
| 12 |
| x |
| 4 |
| x |
| 12 |
| 1 |
| 48 |


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A��
| ||
B��
| ||
C��
| ||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
| �� |
| 2 |
| b |
| a |
| b |
A����-
| ||
B��
| ||
C��
| ||
| D���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
A��
| ||
B��
| ||
C��
| ||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A����ֱ�Ҫ���� |
| B����ֲ���Ҫ���� |
| C����Ҫ��������� |
| D���Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
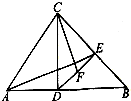 ��ͼ�������������ABC�У�DΪC��AB�ϵ���Ӱ��EΪD��BC�ϵ���Ӱ��FΪDE��һ�㣬������
��ͼ�������������ABC�У�DΪC��AB�ϵ���Ӱ��EΪD��BC�ϵ���Ӱ��FΪDE��һ�㣬������| EF |
| FD |
| AD |
| DB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| sin�� | ||
1+
|
| cos�� |
| 1+tan�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| (x- a)( x- a2+ a) |
| x - a |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com