
| (x- a)( x- a2+ a) |
| x - a |
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
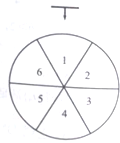 商场销售的某种饮品每件售价36元,成本为20元.对该饮品进行促销;顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针指向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其它情况无奖.
商场销售的某种饮品每件售价36元,成本为20元.对该饮品进行促销;顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针指向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其它情况无奖.| x |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| b |
| a |
| b |
| π |
| 3 |
| 3 |
| 7 |
| ||
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com