
分析 由已知式子和二倍角公式可得sinα,进而可得cosα,再由切化弦和二倍角公式代值计算可得.
解答 解:∵5sin2α=6cosα,∴10sinαcosα=6cosα,
∵α∈(0,$\frac{π}{2}$),∴cosα≠0,∴$sinα=\frac{3}{5}$,
∴由同角三角函数基本关系可得cosα=$\frac{4}{5}$,
∴$tan\frac{α}{2}=\frac{{sin\frac{α}{2}}}{{cos\frac{α}{2}}}=\frac{{2{{sin}^2}\frac{α}{2}}}{{2sin\frac{α}{2}cos\frac{α}{2}}}=\frac{1-cosα}{sinα}=\frac{{1-\frac{4}{5}}}{{\frac{3}{5}}}=\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查二倍角的正弦和正切公式,涉及同角三角函数基本关系,属中档题.


科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(文)试卷(解析版) 题型:解答题
已知抛物线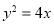 的焦点为
的焦点为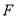 ,过点
,过点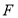 的直线交抛物线于
的直线交抛物线于 两点.
两点.
(1)若 ,求直线
,求直线 的斜率;
的斜率;
(2)设点 在线段
在线段 上运动,原点
上运动,原点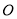 关于点
关于点 的对称点为
的对称点为 ,求四边形
,求四边形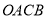 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(年份) | 2012 | 2013 | 2014 | 2015 | 2016 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
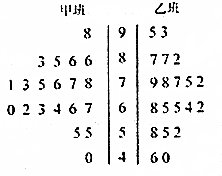 甲、乙两班各20个学生某次数学考试成绩(单位:分)的茎叶图如图所示,根据茎叶图解决下列问题.
甲、乙两班各20个学生某次数学考试成绩(单位:分)的茎叶图如图所示,根据茎叶图解决下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com