
| x(年份) | 2012 | 2013 | 2014 | 2015 | 2016 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
分析 (1)先做出两组数据的平均数,把平均数和条件中所给的两组数据代入求解b的公式,做出b的值,再求出a的值,写出回归直线的方程.
(2)把x=2020代入直线的方程得到y=12.38,估计维修的费用.这是一个预报值,不是正确数值
解答 解1:(1)$\bar x$=$\frac{1}{5}$(2012+2013+2014+2015+2016)=2014,
$\bar y$=$\frac{1}{5}$(2.2+3.8+5.5+6.55+7)=5,
$\sum_{i=1}^5{({x_i}-\bar x)({y_i}-\bar y)}=12.3$,$\sum_{i=1}^5{{{({x_i}-\bar x)}^2}}=10$,
∴$\hat b=\frac{{\sum_{i=1}^5{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^5{{{({x_i}-\bar x)}^2}}}}=1.23$$\hat a=\bar y-\hat b\overline{x}=-2472.22$,
∴$所求的回归直线方程为\hat y=1.23x-2472.22$
另解:设X=x-2014,Y=y-5.5 则
| X | -2 | -1 | 0 | 1 | 2 |
| Y | -3.3 | -1.7 | 0 | 1 | 1.5 |
点评 本题考查线性回归方程的求解和应用,是一个基础题,解题的关键是正确应用最小二乘法来求线性回归方程的系数.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:选择题
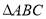 中,“角
中,“角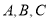 成等差数列”是“
成等差数列”是“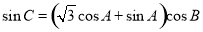 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图.
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
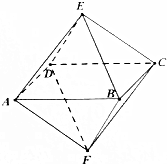 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com