
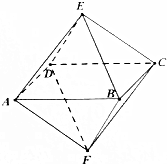
 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 利用直线和直所成的角以及利用等积法求点A到平面BCE的距离.
解答 解:因为八面体的各条棱长均为1,四边形ABCD为正方形,
所以在四棱锥E-ABCD中,相邻两条侧棱所成的角为60°,而像AE与CE所成的角为90°,因为AE=CE=1,AC=$\sqrt{2}$,满足勾股定理的逆定理,所以AE⊥CE,同理AF⊥CF,AE⊥AF,所以四边形AECF是正方形;故①②正确;
设点A到平面BCE的距离h,由VE-ABCD=2VA-BCE,
所以$\frac{1}{3}×1×1×\frac{\sqrt{2}}{2}=2×\frac{1}{3}×\frac{\sqrt{3}}{4}h$,解得h=$\frac{\sqrt{6}}{3}$;
所以点A到平面BCE的距离$\frac{\sqrt{6}}{3}$;故③错误;
故选:C.
点评 本题考查了立体几何中线线关系以及线面关系,利用了等积法求点到平面的距离.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
| x(年份) | 2012 | 2013 | 2014 | 2015 | 2016 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {-3,-1} | C. | {-3,-1,0} | D. | {0,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com