
分析 利用诱导公式化简函数的表达式,通过两角和的正弦函数化为一个角的一个三角函数的形式,求出周期,通过(1)得到的函数表达式,利用正弦函数的最值,求出函数的最大值.
解答 解:∵f(x)=3cos($\frac{π}{2}$-x)+$\sqrt{3}$sin($\frac{π}{2}$+x)
=3sinx+$\sqrt{3}$cosx
=2$\sqrt{3}$($\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)
=2$\sqrt{3}$(sinxcos$\frac{π}{6}$+sin$\frac{π}{6}$cosx)
=2$\sqrt{3}$sin(x+$\frac{π}{6}$),
∴T=2π.
当sin(x+$\frac{π}{6}$)=1时,
函数f(x)取最大值为:2$\sqrt{3}$.
故答案为:2π;$2\sqrt{3}$.
点评 本题考查利用诱导公式、两角和的正弦函数化简三角函数的表达式的方法,考查三角函数的最值、周期的求法,考查计算能力,是基础题.


科目:高中数学 来源: 题型:解答题
 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图.
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次.得到甲、乙两位学生成绩的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{2}$ | B. | π | C. | $\frac{π}{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
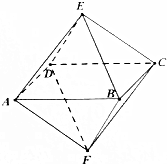 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,平面上有一组间距为5的平行线(无数条),把一根长为2的针投到平面上,我们可以通过下面的方法计算这根针与其中一条直线相交的概率:设针的中点到距其最近的一条直线的距离为d,针所在的倾斜角为θ,则d≤sinθ时,针与该直线有公共点.根据这种方法,计算出相应的概率为$\frac{4}{5π}$.
如图,平面上有一组间距为5的平行线(无数条),把一根长为2的针投到平面上,我们可以通过下面的方法计算这根针与其中一条直线相交的概率:设针的中点到距其最近的一条直线的距离为d,针所在的倾斜角为θ,则d≤sinθ时,针与该直线有公共点.根据这种方法,计算出相应的概率为$\frac{4}{5π}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com