
某家电专卖店在五一期间设计一项有奖促销活动,每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
| 奖次 | 一等奖 | 二等奖 | 三等奖 |
| 随机数组的特征 | 3个1或3个0 | 只有2个1或2个0 | 只有1个1或1个0 |
| 资金(单位:元) | 5m | 2m | m |
(1)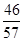 ;(2)(ⅰ)
;(2)(ⅰ) ,(ⅱ)400.
,(ⅱ)400.
解析试题分析:解题思路:(1)利用对立事件的概率与古典概型的概率公式求解即可;(2)(ⅰ)根据二项分布的概率公式求解;(ⅱ)平均奖金即随机奖金的数学期望.规律总结:1.遇到“至少”、“至多”,且正面情况较多时,可以考虑对立事件的概率;2.利用概率或随机变量的分布列以及期望、方差解决应用题时,要注意随机变量的实际意义.
试题解析:(1)在20组数中,获奖的数组有8组,
记“至少有1组获奖”为事件A,则 .
.
(2)(ⅰ)购买一台电视机获奖的概率为 ,
,
则购买的四台电视恰好有两台获奖的概率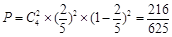 .
.
(ⅱ)记每台电视的奖金为随机变量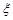 ,则
,则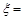 0,m,2m,5m.
0,m,2m,5m.
由题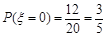 ;
; ;
;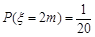 ;
;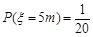 .
.
则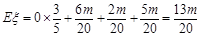 ,
,
由于平均每台电视的奖金不超过260元,
所以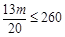 ,解得
,解得 ,
,
故本次活动平均每台电视的奖金不超过260元时,m的最大值是400元.
考点:1.古典概型;2.二项分布;3.随机变量的数学期望.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:填空题
若随机变量X服从两点分布,且成功概率为0.7;随机变量Y服从二项分布,且Y~B(10,0.8),则EX,DX,EY,DY分别是........,........,........,.........
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校举行综合知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有6次答题的机会,选手累计答对4题或答错3题即终止其初赛的比赛,答对4题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为 (已知甲回答每道题的正确率相同,并且相互之间没有影响).
(已知甲回答每道题的正确率相同,并且相互之间没有影响).
(Ⅰ)求选手甲回答一个问题的正确率;
(Ⅱ)求选手甲可以进入决赛的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
同时抛掷4枚均匀的硬币80次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为 .
.
(1)求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
(2)求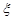 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区为了解高二学生作业量和玩电脑游戏的情况,对该地区内所有高二学生采用随机抽样的方法,得到一个容量为200的样本.统计数据如下:
(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂在试验阶段大量生产一种零件,这种零件有 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为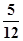 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为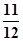 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽取该种零件 个,设
个,设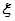 表示其中合格品的个数,求
表示其中合格品的个数,求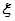 的分布列及数学期望
的分布列及数学期望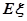 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
 .(12分)
.(12分) ,求
,求 的分布列与期望.
的分布列与期望. | 0.15 | 0.10 | 0.05[ | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对每道甲类题的概率都是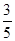 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是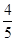 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用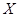 表示张同学答对题的个数,求
表示张同学答对题的个数,求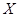 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
乒乓球台面被球网分成甲、乙两部分,如图,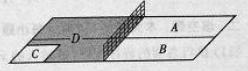 甲上有两个不相交的区域
甲上有两个不相交的区域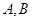 ,乙被划分为两个不相交的区域
,乙被划分为两个不相交的区域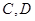 .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在
.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在 上记3分,在
上记3分,在 上记1分,其它情况记0分.对落点在
上记1分,其它情况记0分.对落点在 上的来球,队员小明回球的落点在
上的来球,队员小明回球的落点在 上的概率为
上的概率为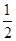 ,在
,在 上的概率为
上的概率为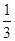 ;对落点在
;对落点在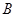 上的来球,小明回球的落点在
上的来球,小明回球的落点在 上的概率为
上的概率为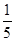 ,在
,在 上的概率为
上的概率为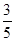 .假设共有两次来球且落在
.假设共有两次来球且落在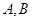 上各一次,小明的两次回球互不影响.求:
上各一次,小明的两次回球互不影响.求:
(Ⅰ)小明的两次回球的落点中恰有一次的落点在乙上的概率;
(Ⅱ)两次回球结束后,小明得分之和 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com