
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
【答案】(1)a![]() ;(2)不存在,理由见解析.
;(2)不存在,理由见解析.
【解析】
(1)对原函数求导,根据导数和函数的单调性的关系即可求出![]() 的取值范围;
的取值范围;
(2)问题转化为即![]() 在
在![]() 时恒成立,令
时恒成立,令![]() ,
,![]() 求导后分
求导后分![]() 和
和![]() 求函数的单调区间,进一步求得函数的最值得答案.
求函数的单调区间,进一步求得函数的最值得答案.
解:(1)![]() 函数
函数![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,
![]() 在
在![]() ,
,![]() 上恒成立,
上恒成立,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
![]() ;
;
(2)![]() ,
,
![]() (1)
(1)![]() ,
,
![]() 函数
函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() 不等式
不等式![]() 在
在![]() 时恒成立,
时恒成立,
![]() 在
在![]() 时恒成立,
时恒成立,
即![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增,
上单调递增,
![]() (1)
(1)![]() ,则
,则![]() ,矛盾,
,矛盾,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
![]() 在
在![]() 单调递减,在
单调递减,在![]() ,
,![]() 单调递增,
单调递增,
![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
![]() ,
,
![]() 不存在整数
不存在整数![]() 使得
使得![]() 恒成立,
恒成立,
综上所述不存在满足条件的整数![]() .
.


科目:高中数学 来源: 题型:
【题目】在某中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知第二小组的频数是40.

(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数;
(3)求这两个班参赛学生的成绩的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,各个侧面均是边长为
中,各个侧面均是边长为![]() 的正方形,
的正方形,![]() 为线段
为线段![]() 的中点.
的中点.
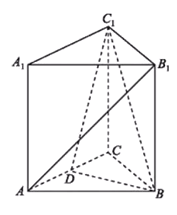
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)设![]() 为线段
为线段![]() 上任意一点,在
上任意一点,在![]() 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的不断发展,手机打车软件APP也不断推出.在某地有AB两款打车APP,为了调查这两款软件叫车后等候的时间,用这两款APP分别随机叫了50辆车,记录了候车时间如下表:
A款软件:
候车时间(分钟) |
|
|
|
|
|
|
车辆数 | 2 | 12 | 8 | 12 | 14 | 2 |
B款软件:
候车时间(分钟) |
|
|
|
|
|
|
车辆数 | 2 | 10 | 28 | 7 | 2 | 1 |
(1)试画出A款软件候车时间的频率分布直方图,并估计它的众数及中位数;
(2)根据题中所给的数据,将频率视为概率
(i)能否认为B款软件打车的候车时间不超过6分钟的概率达到了75%以上?
(ii)仅从两款软件的平均候车时间来看,你会选择哪款打车软件?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一幅标准的三角板如图(1)中,![]() 为直角,
为直角,![]() ,
,![]() 为直角,
为直角,![]() ,且
,且![]() ,把
,把![]() 与
与![]() 拼齐使两块三角板不共面,连结
拼齐使两块三角板不共面,连结![]() 如图(2).
如图(2).
(1)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() ;
;
(2)在《九章算术》中,称四个面都是直角三角形的三棱锥为“鳖臑”,若图(2)中![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,则图(2)是否为鳖臑?说明理由.
,则图(2)是否为鳖臑?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com