
【题目】已知函数 ,若存在实数
,若存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根,则实数
有两个不同的实根,则实数![]() 的取值范围是()
的取值范围是()
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
【答案】C
【解析】
若存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根,等价于存在实数k,使函数
有两个不同的实根,等价于存在实数k,使函数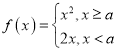 与函数
与函数![]() 的图象有两个不同的交点,然后对
的图象有两个不同的交点,然后对![]() 分四种情况讨论,作出函数
分四种情况讨论,作出函数![]() 的图象,根据图象可以得到实数
的图象,根据图象可以得到实数![]() 的范围.
的范围.
联立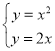 ,解得
,解得![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
如图:
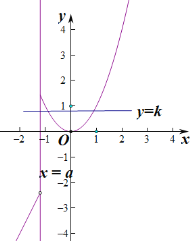
由图可知,存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根.
有两个不同的实根.
当![]() 时,函数
时,函数![]() 在R上递增,
在R上递增,
如图:
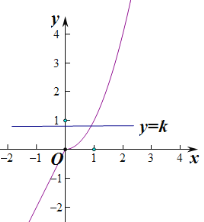
由图可知,不存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根.
有两个不同的实根.
当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上也递增,并且
上也递增,并且![]() ,
,
如图:
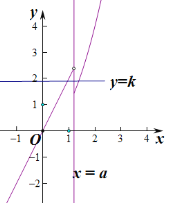
由图可知, 存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根;
有两个不同的实根;
当![]() 时,
时,![]() 在R上是增函数,
在R上是增函数,
如图:
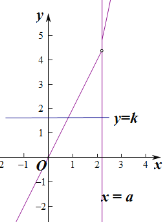
由图可知,不存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根.
有两个不同的实根.
综上所述: 实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
故选C.


科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且c= ![]() asinC﹣ccosA
asinC﹣ccosA
(1)求A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xetx﹣ex+1,其中t∈R,e是自然对数的底数.
(1)若方程f(x)=1无实数根,求实数t的取值范围;
(2)若函数f(x)在(0,+∞)内为减函数,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面推理过程中使用了类比推理方法,其中推理正确的是( )
A. 平面内的三条直线![]() ,若
,若![]() ,则
,则![]() .类比推出:空间中的三条直线
.类比推出:空间中的三条直线![]() ,若
,若![]() ,则
,则![]()
B. 平面内的三条直线![]() ,若
,若![]() ,则
,则![]() .类比推出:空间中的三条向量
.类比推出:空间中的三条向量![]() ,若
,若![]() ,则
,则![]()
C. 在平面内,若两个正三角形的边长的比为![]() ,则它们的面积比为
,则它们的面积比为![]() .类比推出:在空间中,若两个正四面体的棱长的比为
.类比推出:在空间中,若两个正四面体的棱长的比为![]() ,则它们的体积比为
,则它们的体积比为![]()
D. 若![]() ,则复数
,则复数![]() .类比推理:“若
.类比推理:“若![]() ,则
,则![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面ADC∥平面A1B1C1 , B为线段AD的中点,△ABC≈△A1B1C1 , 四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A= ![]() ,M为棱A1C1的中点.
,M为棱A1C1的中点.
(Ⅰ)若N为线段DC1上的点,且直线MN∥平面ADB1A1 , 试确定点N的位置;
(Ⅱ)求平面MAD与平面CC1D所成的锐二面角的余弦值.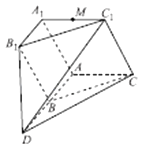
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com