
【题目】将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.![]()
D.![]()
【答案】C
【解析】解:将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,可得函数y=3sin(2x+
)图象上所有点的横坐标伸长到原来的2倍,可得函数y=3sin(2x+ ![]() )的图象,
)的图象,
再向右平移 ![]() 个单位长度,可得y=3sin[2(x﹣
个单位长度,可得y=3sin[2(x﹣ ![]() )+
)+ ![]() ]=3sin(2x﹣
]=3sin(2x﹣ ![]() )的图象,故g(x)=3sin(2x﹣
)的图象,故g(x)=3sin(2x﹣ ![]() ).
).
令 2x﹣ ![]() =kπ+
=kπ+ ![]() ,k∈z,得到 x=
,k∈z,得到 x= ![]() π+
π+ ![]() ,k∈z.
,k∈z.
则得 y=g(x)图象的一条对称轴是 ![]() ,
,
故选:C.
【考点精析】根据题目的已知条件,利用正弦函数的对称性和函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握正弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() ;图象上所有点向左(右)平移
;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】高考数学试题中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的.评分标准规定:“每题只选1项,答对得5分,不答或答错得0分.”某考生每道题都给出了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(1)得50分的概率;
(2)得多少分的可能性最大;
(3)所得分数ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸四边形PABQ中,其中A,B为定点,AB= ![]() ,P,Q为动点,满足AP=PQ=QB=1.
,P,Q为动点,满足AP=PQ=QB=1.
(1)写出cosA与cosQ的关系式;
(2)设△APB和△PQB的面积分别为S和T,求S2+T2的最大值,以及此时凸四边形PABQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AD=BD,平面AA1C1C⊥平面ABB1A1 , A1C1= ![]() AA1 , ∠C1A1A=
AA1 , ∠C1A1A= ![]() .
. 
(1)若E,F分别为C1B1 , AC的中点,求证:EF∥平面ABB1A1;
(2)求平面A1B1C1与平面CB1D所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1= ![]() (n∈N*),若bn+1=(n﹣2λ)(
(n∈N*),若bn+1=(n﹣2λ)( ![]() +1)(n∈N*),b1=﹣λ,且数列{bn}是单调递增数列,則实数λ的取值范围是( )
+1)(n∈N*),b1=﹣λ,且数列{bn}是单调递增数列,則实数λ的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为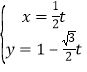 (t为参数
(t为参数![]() 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为
以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 判断直线l与圆C的交点个数;
判断直线l与圆C的交点个数;
![]() Ⅱ
Ⅱ![]() 若圆C与直线l交于A,B两点,求线段AB的长度.
若圆C与直线l交于A,B两点,求线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲所示,放在水平地面上的物体,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物体运动速度v与时间t的关系如图乙所示.下列判断正确的是:
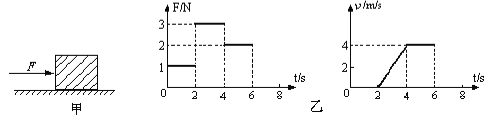
A.t=3s时,物体受到力的合力为零
B.t=6s时,将F撤掉,物体立刻静止
C.2s~4s内物体所受摩擦力逐渐增大
D.t=1s时,物体所受摩擦力是1N
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com