
某个实心零部件的形状是如下图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台 ,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱
,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱 .
.

(1)证明:直线 平面
平面 ;
;
(2)现需要对该零部件表面进行防腐处理.已知 ,
, ,
, ,
, (单位:
(单位: ),每平方厘米的加工处理费为
),每平方厘米的加工处理费为 元,需加工处理费多少元?
元,需加工处理费多少元?
(1)详见解析;(2)所需加工处理费为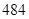 元.
元.
【解析】
试题分析:(1)先证 ,再证
,再证 平面
平面 ,从而得到
,从而得到 平面
平面 ,在证明
,在证明 平面
平面 的过程中,利用四边形
的过程中,利用四边形 为正方形得到
为正方形得到 ,再由直棱柱的性质得到
,再由直棱柱的性质得到 平面
平面 ,从而得到
,从而得到 ,再利用直线与平面垂直的判定定理得到
,再利用直线与平面垂直的判定定理得到 平面
平面 ;(2)先计算该几何体的表面积,然后利用单价乘以表面积便可以得到加工处理费.
;(2)先计算该几何体的表面积,然后利用单价乘以表面积便可以得到加工处理费.
试题解析:(1)因为四棱柱ABCD-A2B2C2D2的侧面是全等的矩形,
所以AA2⊥AB,AA2⊥AD,又因为AB∩AD=A,所以AA2⊥平面ABCD.
连接BD,因为BD⊂平面ABCD,所以AA2⊥BD.
因为底面ABCD是正方形,所以AC⊥BD.
根据棱台的定义可知,BD与B1D1共面.
又已知平面ABCD∥平面A1B1C1D1,且平面BB1D1D∩平面ABCD=BD,
平面BB1D1D∩平面A1B1C1D1=B1D1,所以B1D1∥BD.于是
由AA2⊥BD,AC⊥BD,B1D1∥BD,可得AA2⊥B1D1,AC⊥B1D1,
又因为AA2∩AC=A,所以B1D1⊥平面ACC2A2.
(2)因为四棱柱ABCD-A2B2C2D2的底面是正方形,侧面是全等的矩形,
所以S1=S四棱柱上底面+S四棱柱侧面=(A2B2)2+4AB·AA2=102+4×10×30=1 300(cm2).
又因为四棱台A1B1C1D1-ABCD的上、下底面均是正方形,侧面是全等的等腰梯形.
所以S2=S四棱台下底面+S四棱台侧面
=(A1B1)2+4× (AB+A1B1)h等腰梯形的高
(AB+A1B1)h等腰梯形的高
=202+4× (10+20)
(10+20)
=1120(cm2).
于是该实心零部件的表面积为S=S1+S2=1300+1120=2420(cm2),
故所需加工处理费为0.2S=0.2×2420=484(元).
考点:1.直线与平面垂直;2.空间几何体的表面积


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
 (2012•湖北)某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.
(2012•湖北)某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.查看答案和解析>>
科目:高中数学 来源: 题型:
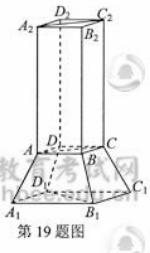
某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCD-A2B2C2D2。
(1) 证明:直线B1D1⊥平面ACC2A2;
(2) 现需要对该零部件表面进行防腐处理,已知AB=10,A1B1=20,AA2=30,AA1=13(单位:厘米),每平方厘米的加工处理费为0.20元,需加工处理费多少元?
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(湖北卷解析版) 题型:解答题
某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台 ,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱
,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱 。
。

(1) 证明:直线 平面
平面 ;
;
(2)现需要对该零部件表面进行防腐处理,已知 (单位:厘米),每平方厘米的加工处理费为
(单位:厘米),每平方厘米的加工处理费为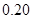 元,需加工处理费多少元?
元,需加工处理费多少元?
查看答案和解析>>
科目:高中数学 来源:2012年湖北省高考数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com