练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若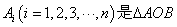所在的平面内的点，且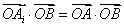.给出下列说法：

    ①；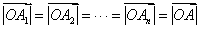

    ②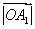的最小值一定是；

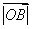    ③点A、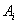在一条直线上；

    ④向量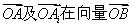的方向上的投影必相等.

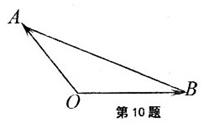
    其中正确的个数是

    A.1个       B.2个       C.3个       D.4个



    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在△ABC中，角A，B，C的对边分别是a，b，c，a＝8，b＝10，△ABC的面积为20，则△ABC的最大角的正切值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列命题正确的是                                                  （    ）

    A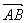．与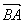是两平行向量          

    B．若a、b都是单位向量,则a=b

    C．若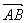=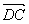,则A、B、C、D四点构成平行四边形

    D．两向量相等的充要条件是它们的始点、终点相同

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知非零向量a,b,c满足a+b+c=0,向量a,b的夹角为120°,且|b|=2|a|求向量a与

    c的夹角。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正三棱锥V-ABC的主视图、俯视图如下图所示，其中，则该三棱锥的左视图的面积为

    A.9     B.6     C.  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    双曲线的左右焦点为，P是双曲线左支上一点，满足相切，则双曲线的离心率e为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC中，角A，B，C的对边分别为a，b，c，且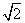acos B＝ccos B＋bcos C.

    (1)求角B的大小；

    (2)设向量m＝(cos A，cos 2A)，n＝(12，－5)，求当m·n取最大值时，tan C的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前三项分别为a1＝5，a2＝6，a3＝8，且数列{an}的前n项和Sn满足Sn＋m＝(S2n＋S2m)－(n－m)2，其中m，n为任意正整数．

    (1)求数列{an}的通项公式及前n项和Sn；

    (2)求满足S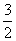－an＋33＝k2的所有正整数k，n.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    我们把形如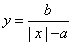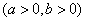的函数称为“莫言函数”，并把其与y轴的交点关于原

        点的对称点称为“莫言点”，以“莫言点”为圆心，凡是与“莫言函数”图像有公共点的圆，

        皆称之为“莫言圆”，当a=b=l时，在所有的“莫言圆”中，面积的最小值为____．

    查看答案和解析>>

    同步练习册答案