练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知△ABC中，角A，B，C的对边分别为a，b，c，且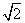acos B＝ccos B＋bcos C.

    (1)求角B的大小；

    (2)设向量m＝(cos A，cos 2A)，n＝(12，－5)，求当m·n取最大值时，tan C的值．


    解　(1)由题意，sin Acos B＝sin Ccos B＋cos Csin B，(2分)

    所以sin Acos B＝sin(B＋C)＝sin(π－A)＝sin A．(3分)

    因为0＜A＜π，所以sin A≠0.

    所以cos B＝.(5分)

    因为0＜B＜π，所以B＝.

    (2)因为m·n＝12cos A－5cos 2A，

    所以m·n＝－10cos2A＋12cos A＋5

      ＝－10＋.

    所以当cos A＝时，m·n取最大值．

    此时sin A＝(0＜A＜)，于是tan A＝.

    所以tan C＝－tan(A＋B)＝－＝7


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    下图是一个算法的流程图，最后输出的S＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    的振幅为          初相为         。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


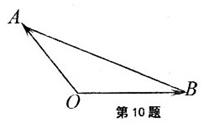
    若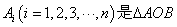所在的平面内的点，且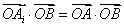.给出下列说法：

    ①；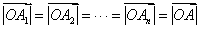

    ②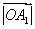的最小值一定是；

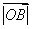    ③点A、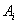在一条直线上；

    ④向量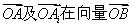的方向上的投影必相等.

    其中正确的个数是

    A.1个       B.2个       C.3个       D.4个


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在盒子里有大小相同，仅颜色不同的乒乓球共10个，其中红球5个，白球3个，蓝球2个.现从中任取出一球确定颜色后放回盒子里，再取下一个球.重复以上操作，最多取3次，过程中如果取出蓝色球则不再取球.

    求：（I）最多取两次就结束的概率；

       （II）整个过程中恰好取到2个白球的概率；

       （III）取球次数X的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知无穷数列{an}的各项均为正整数，Sn为数列{an}的前n项和．

    (1)若数列{an}是等差数列，且对任意正整数n都有Sn3＝(Sn)3成立，求数列{an}的通项公式；

    (2)对任意正整数n，从集合{a1，a2，…，an}中不重复地任取若干个数，这些数之间经过加减运算后所得数的绝对值为互不相同的正整数，且这些正整数与a1，a2，…，an一起恰好是1至Sn全体正整数组成的集合．

    (ⅰ)求a1，a2的值；

    (ⅱ)求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设向量a＝(2，sin θ)，b＝(1，cos θ)，θ为锐角．

    (1)若a·b＝，求sin θ＋cos θ的值；

    (2)若a∥b，求sin的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    第22届冬季奥运会于2014年2月7日在俄罗斯索契开幕，到冰壶比赛场馆服务的大学生志愿者中，有2名来自莫斯科国立大学，有4名来自圣彼得堡国立大学，现从这6名志愿者中随机抽取2人，至少有1名志愿者来自莫斯科国立大学的概率是（    ）

        A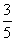．      B．       C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    运行如图1的程序框图，则输出s的结果是

    A.           B.           C.        D.

    查看答案和解析>>

    同步练习册答案