练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设向量a＝(2，sin θ)，b＝(1，cos θ)，θ为锐角．

    (1)若a·b＝，求sin θ＋cos θ的值；

    (2)若a∥b，求sin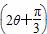的值．


    解　(1)因为a·b＝2＋sin θcos θ＝，

    所以sin θcos θ＝.(2分)

    所以(sin θ＋cos θ)2＝1＋2sin θcos θ＝.

    又因为θ为锐角，所以sin θ＋cos θ＝.(5分)

    (2)法一　因为a∥b，所以tan θ＝2.(7分)

    所以sin 2θ＝2sin θcos θ＝＝，

    cos 2θ＝cos2θ－sin2θ＝＝－.(11分)

    法二　因为a∥b，所以tan θ＝2.(7分)

    所以sin θ＝，cos θ＝.

    因此sin 2θ＝2sin θcos θ＝，

    cos 2θ＝cos2θ－sin2θ＝－.(11分)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    抛物线y2= 4x上一点P到焦点F的距离是10, 则P点的坐标是（   ）

       A．（9, 6）      B．（6, 9）      C．（±6, 9）          D．（9,±6）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正三棱锥V-ABC的主视图、俯视图如下图所示，其中，则该三棱锥的左视图的面积为

    A.9     B.6     C.  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC中，角A，B，C的对边分别为a，b，c，且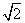acos B＝ccos B＋bcos C.

    (1)求角B的大小；

    (2)设向量m＝(cos A，cos 2A)，n＝(12，－5)，求当m·n取最大值时，tan C的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在四棱锥P ­ABCD中，PA⊥底面ABCD，AC⊥CD，∠DAC＝60°，AB＝BC＝AC，E是PD的中点，F为ED的中点．

    (1)求证：平面PAC⊥平面PCD；

    (2)求证：CF∥平面BAE.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前三项分别为a1＝5，a2＝6，a3＝8，且数列{an}的前n项和Sn满足Sn＋m＝(S2n＋S2m)－(n－m)2，其中m，n为任意正整数．

    (1)求数列{an}的通项公式及前n项和Sn；

    (2)求满足S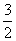－an＋33＝k2的所有正整数k，n.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若（a－4i）i=b－i，（a，b∈R，i为虚数单位），则复数z=a+bi在复平面内的对应点位于（    ）

        A．第一象限    B．  第二象限       C．第三象限    D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知各项均为正数的等比数列{an}满足a3 =8，a5 +a7=160，{an}的前n项和为Sn．

      （I）求an；

      （II）若数列{bn}的通项公式为bn=（-1）n·n（n∈N+），求数列{an·bn}的前n项和Tn。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在中，已知且．

    （1）求角B和的值；

    （2）若的边，求边AC的长．

    查看答案和解析>>

    同步练习册答案