
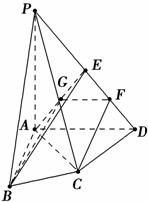
如图,在四棱锥P ABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.
(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.

证明 (1)因为PA⊥底面ABCD,所以PA⊥CD,(2分)
又AC⊥CD,且AC∩PA=A,所以CD⊥平面PAC,(4分)
 又CD⊂平面PCD,所以平面PAC⊥平面PCD.(7分)
又CD⊂平面PCD,所以平面PAC⊥平面PCD.(7分)
(2 )取AE中点G,连接FG,BG.
)取AE中点G,连接FG,BG.
因为F为ED的中点,所以FG∥AD且FG=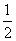 AD.(9分)
AD.(9分)
在△ACD中,AC⊥CD,∠DAC=60°,
所以AC=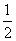 AD,所以BC=
AD,所以BC=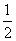 AD.(11分)
AD.(11分)
在△ABC中,AB=BC=AC,所以∠ACB=60°,
从而∠ACB=∠DAC,所以AD∥BC.
综上,FG∥BC,FG=BC,四边形FGBC为平行四边形,所以CF∥BG.(13分)
又BG⊂平面BAE,CF⊄平面BAE,所以CF∥平面BAE.(14分)


科目:高中数学 来源: 题型:
下列命题中真命题的个数是( )
①“∀x∈R,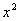 -x>0”的否定是“∃x∈R,
-x>0”的否定是“∃x∈R,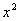 -x<0”;② ∀x∈
-x<0”;② ∀x∈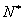 ,
,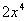
+1是奇数;③若|2x-1|>1,则0< <1或
<1或 <0.
<0.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球.
求:(I)最多取两次就结束的概率;
(II)整个过程中恰好取到2个白球的概率;
(III)取球次数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池 ,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的PQRS面积为S2.
,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的PQRS面积为S2.
(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求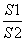 的最小值.
的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com