对于函数y=f(x)与常数a,b,若f(2x)=af(x)+b恒成立,则称(a,b)为函数f(x)的一个“P数对”.设函数f(x)的定义域为R+,且f(1)=3.
(1)若(1,1)是f(x)的一个“P数对”,求f(210);
(2)若(-2,0)是f(x)的一个“P数对”,且当x∈[1,2)时f(x)=k(2-x),求f(x)在区间[1,22n)(n∈N*)上的最大值与最小值;
(3)若f(x)是增函数,且(2,-2)是f(x)的一个“P数对”,试比较下列各组中两个式子的大小,并说明理由. ①f(2-n)与2-n+2(n∈N*);②f(x)与2x+2(x∈(2-n,21-n],n∈N*).
【答案】
分析:(1)由已知,f(2x)=f(x)+1恒成立,整理f(2x)-f(x)=1,令x=2
k,则f(2
k+1)-f(2
k)=1,{f(2
k)}是等差数列,利用通项公式求解;
(2)先确定f(x)在[1,2)上的取值范围是(0,3],再利用f(2x)=-2f(x)恒成立,当x∈[2
k-1,2
k)(k∈N
*)时,
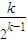
∈[1,2),f(x)=-2
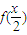
=…=
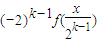
,即可得出结论;
(3)①f(x)=

f(2x)+1恒成立,令x=
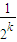
,则f(
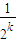
)=

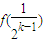
+1,可得{
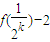
}是一个等比数列,可得结论;
②当x∈[2
-n,2
1-n]时,由f(x)是增函数,故f(x)≤f(2
1-n)=2
1-n+2,从而可得结论.
解答:解:(1)若(1,1)是f(x)的一个“P数对”,即f(2x)=f(x)+1恒成立,整理f(2x)-f(x)=1,令x=2
k,则f(2
k+1)-f(2
k)=1,
所以f(2),f(4),f(8),…f(2
n)构成公差为1的等差数列,
令x=1得f(2)=f(1)+1=4,所以f(2
n)=4+(n-1)×1=n+3
所以f(2
10)=10+3=13;
(2)x∈[1,2)时,f(x)=k(2-x),令x=1,则f(1)=k=3,即当x∈[1,2)时,f(x)=3(2-x),所以f(x)在[1,2)上的取值范围是(0,3],
又(-2,0)是f(x)的一个“P数对”,即f(2x)=-2f(x)恒成立,当x∈[2
k-1,2
k)(k∈N
*)时,
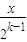
∈[1,2),f(x)=-2
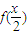
=…=
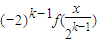
,
∴故当k为奇数时,f(x)在[2
k-1,2
k)上的取值范围是(0,3×2
k-1]
当k为偶数时,f(x)在[2
k-1,2
k)上的取值范围是[-3×2
k-1,0)
所以,f(x)在区间[1,2
2n)上的最大值为3×2
2n-2,最小值为-3×2
2n-1.
(3)①(2,-2)是f(x)的一个“类P数对”,可知f(2x)=2f(x)-2恒成立.
即f(x)=

f(2x)+1恒成立
令x=
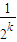
,则f(
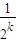
)=

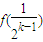
+1
∴
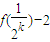
=

[
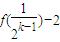
]
∵
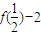
=f(1)-2=1
∴{
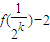
}是一个等比数列,
∴
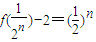
∴f(2
-n)=2
-n+2
②当x∈[2
-n,2
1-n]时,由f(x)是增函数,故f(x)≤f(2
1-n)=2
1-n+2
∵x>2
-n,∴2x+2>2
1-n+2,∴f(x)<2x+2.
点评:本题考查利用新定义分析问题、解决问题的能力.考查转化计算,分类讨论、构造能力及推理论证能力,思维量大,属于难题.

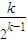 ∈[1,2),f(x)=-2
∈[1,2),f(x)=-2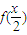 =…=
=…=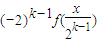 ,即可得出结论;
,即可得出结论; f(2x)+1恒成立,令x=
f(2x)+1恒成立,令x=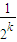 ,则f(
,则f(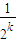 )=
)=
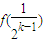 +1,可得{
+1,可得{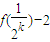 }是一个等比数列,可得结论;
}是一个等比数列,可得结论;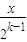 ∈[1,2),f(x)=-2
∈[1,2),f(x)=-2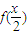 =…=
=…=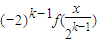 ,
, f(2x)+1恒成立
f(2x)+1恒成立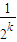 ,则f(
,则f(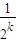 )=
)=
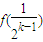 +1
+1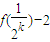 =
= [
[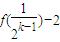 ]
]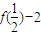 =f(1)-2=1
=f(1)-2=1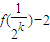 }是一个等比数列,
}是一个等比数列,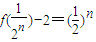


 发散思维新课堂系列答案
发散思维新课堂系列答案