
分析 (1)根据函数的定义域关于原点对称,且f(-x)=-f(x),可得函数f(x)为奇函数.
(2)要解的不等式即f(x)>0,又f(0)=1,分类讨论,根据f(x)的单调性,求得不等式的解集.
解答 解:(1)∵a>0,且a≠1,f(x)=1-$\frac{2}{1+{a}^{x}}$=$\frac{{a}^{x}-1}{{a}^{x}+1}$ 的定义域为R,关于原点对称,
f(-x)=$\frac{{a}^{-x}-1}{{a}^{-x}+1}$=$\frac{1{-a}^{x}}{1{+a}^{x}}$=-f(x),故函数f(x)为奇函数.
(2)不等式f(x)>f(-x),即f(x)>-f(x),即 f(x)>0.
又f(0)=1,
故当a>1时,f(x)为增函数,故不等式f(x)>0的解集为(0,+∞);
当0<a<1时,f(x)为减函数,故不等式f(x)>0的解集为(-∞,0).
点评 本题主要考查函数的奇偶性的判断以及奇函数的性质,函数的单调性的应用,体现了转化、分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
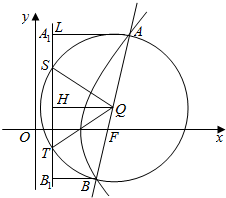 以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:
以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com