练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图为一个正方体与一个半球构成的组合体，半球的底面圆与该正方体的上底面的四边相切， 与正方形的中心重合.将此组合体重新置于一个球中(球未画出)，使该正方体的下底面的顶点均落在球的表面上，半球与球内切，设切点为，若正四棱锥的表面积为，则球的表面积为（ ）

    A.B.C.D.

    【答案】B

    【解析】

    设球，半球的半径分别为，然后用含的式子表示出正方体的棱长与四棱锥的高和四棱锥侧面的高，从而由四棱锥的表面积求出，进而建立关于的方程，求得的值，最后利用球的表面积公式求解即可.

    如图，

    设球，半球的半径分别为， 由题意知正方体的棱长为，四棱锥为正四棱锥.设该正方体的底面的中心为，连接，则四棱锥的高，其各侧面的高为.由题意得，得.易知球的球心在线段上，连接，则在中， ，

    于是由勾股定理，得

    解得，所以球的表面积，

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 过点，且两个焦点的坐标分别为， .

    （1）求的方程；

    （2）若， ， 为上的三个不同的点， 为坐标原点，且，求证：四边形的面积为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是定义域为的函数的导函数，，，则的解集为（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

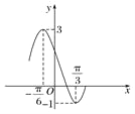
    【题目】已知函数g(x)＝Acos(ωx＋φ)＋B的部分图象如图所示，将函数g(x)的图象保持纵坐标不变，横坐标向右平移个单位长度后得到函数f(x)的图象．求：

    (1)函数f(x)在上的值域；

    (2)使f(x)≥2成立的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD-A1B1C1D1的棱长为2，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的三视图的面积之和最大值为（ ）

    A.6B.7C.8D.9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在中，角的对边分别为,且.

    （1）求的值；

    （2）若,求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的焦点为(，0)，(，0)，且椭圆C过点M(4，1)，直线l：不过点M，且与椭圆交于不同的两点A，B．

    （1）求椭圆C的标准方程；

    （2）求证：直线MA，MB与x轴总围成一个等腰三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的右焦点F与抛物线焦点重合，且椭圆的离心率为，过轴正半轴一点 且斜率为的直线交椭圆于两点.

    （1）求椭圆的标准方程；

    （2）是否存在实数使以线段为直径的圆经过点，若存在，求出实数的值；若不存在说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在城市旧城改造中，某小区为了升级居住环境，拟在小区的闲置地中规划一个面积为的矩形区域（如图所示），按规划要求：在矩形内的四周安排宽的绿化，绿化造价为200元/，中间区域地面硬化以方便后期放置各类健身器材，硬化造价为100元/.设矩形的长为.

    （1）设总造价（元）表示为长度的函数；

    （2）当取何值时，总造价最低，并求出最低总造价.

    查看答案和解析>>

    同步练习册答案