
设数列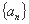 满足
满足 ,且对一切
,且对一切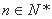 ,有
,有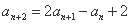
(1) 证明:数列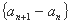 是等差数列;
是等差数列;
(2) 求数列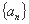 的通项公式;
的通项公式;
(3) 设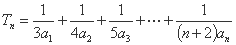 ,求
,求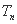 的取值范围。
的取值范围。
科目:高中数学 来源: 题型:
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出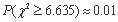 ,则下列说法正确的( )
,则下列说法正确的( )
A.这种疫苗能起到预防甲型H1N1流感的有效率为1%
B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1
C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com