练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在正方体ABCDA1B1C1D1中,求二面角A1BDC1的平面角的余弦值.

    结合空间向量判断或证明线面位置关系



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    对于问题“已知关于x的不等式ax2+bx+c>0的解集为(-1,2),求解关于x的不等式ax2-bx+c>0”,现给出如下一种方法:

    解:由ax2+bx+c>0的解集为(-1,2),得a(-x)2+b(-x)+c>0的解集为(-2,1),即关于x的不等式ax2-bx+c>0的解集为(-2,1).

    参考上述方法,若关于x的不等式+<0的解集为∪,则关于x的不等式+<0的解集为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)=(2+)n,其中n∈N*.若展开式中含x3项的系数为14,则n=　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,已知正方体ABCD-A1B1C1D1的棱长为2,O为底面正方形ABCD的中心,则三棱锥B1BCO的体积=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,正三棱锥OABC底面边长为2,高为1,求该三棱锥的体积及表面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


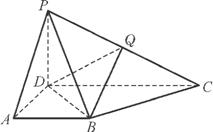
    在四棱锥PABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=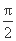,AB=AD=PD=1,CD=2.设Q为侧棱PC上一点,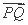=λ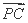,试确定λ的值,使得二面角QBDP的平面角为45°.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     计算:(1) ;　　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知F1,F2分别是椭圆+=1的左、右焦点,点P是椭圆上的任意一点,则的取值范围是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将函数f(x)=sinωx(ω>0)的图象向右平移个单位长度,所得图象经过点,则ω的最小值是　　　　. 

    查看答案和解析>>

    同步练习册答案