
| A. | 关于点(-$\frac{π}{12}$,0)对称 | B. | 关于点($\frac{π}{6}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{2}$对称 |
分析 根据余弦函数f(x)的图象与性质,对选项中的命题进行分析、判断正误即可.
解答 解:函数f(x)=3cos(2x+$\frac{π}{6}$),则
f(-$\frac{π}{12}$)=3cos(-$\frac{π}{6}$+$\frac{π}{6}$)=3≠0,
∴f(x)的图象不关于点(-$\frac{π}{12}$,0)对称,A错误;
f($\frac{π}{6}$)=3cos($\frac{π}{3}$+$\frac{π}{6}$)=0,
∴f(x)的图象关于点($\frac{π}{6}$,0)对称,B正确;
∴f(x)的图象不关于直线x=$\frac{π}{6}$对称,C错误;
f($\frac{π}{2}$)=3cos(π+$\frac{π}{6}$)=-$\frac{3\sqrt{3}}{2}$,
∴f(x)的图象不关于直线x=$\frac{π}{2}$对称,D错误.
故选:B.
点评 本题考查了余弦函数f(x)的图象与性质的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 97+56$\sqrt{3}$ | B. | 144 | C. | 73+40$\sqrt{3}$ | D. | 4p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-1,3] | C. | (-∞,-1]∪[3,+∞) | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | c>b>a | C. | a>b>c | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
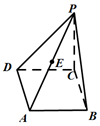 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{5}+\frac{y^2}{10}=1$ | B. | $\frac{x^2}{10}+\frac{y^2}{15}=1$ | C. | $\frac{x^2}{15}+\frac{y^2}{10}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{10}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com