Question

3．已知函数f（x）=$\frac{x}{{e}^{x}}$，给出下列结论：
①（1，+∞）是f（x）的单调递减区间；
②当k∈（-∞，$\frac{1}{e}$）时，直线y=k与y=f（x）的图象有两个不同交点；
③函数y=f（x）的图象与y=x²+1的图象没有公共点．
其中正确结论的序号是（　　）

• A． ①②③
• B． ①③
• C． ①②
• D． ②③

Answer 1

分析 ①先求出函数的导数，令导函数小于0，解出即可判断；②根据函数的单调性画出函数的图象，通过图象读出即可；③求出f（x）的最大值小于y=x²+1的最小值，从而得到答案．

解答 解：①f′（x）=$\frac{1-x}{{e}^{x}}$，令f′（x）＜0，解得：x＞1，
∴函数f（x）在（1，+∞）递减，
故①正确；
②∵f（x）在（-∞，1）递增，在（1，+∞）递减，
∴f（x）_max=f（1）=$\frac{1}{e}$，
x→-∞时，f（x）→-∞，x→+∞时，f（x）→0，
画出函数f（x）的图象，如图示：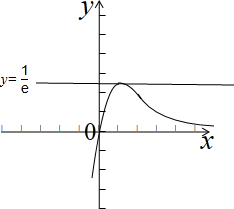
，
∴当k∈（-∞，0）时，直线y=k与y=f（x）的图象有1个不同交点，
当k∈（0，$\frac{1}{e}$）时，直线y=k与y=f（x）的图象有两个不同交点，
故②错误；
③函数f（x）≤$\frac{1}{e}$，而y=x²+1≥1，
∴函数y=f（x）的图象与y=x²+1的图象没有公共点，
故③正确；
故选：①③．

点评 本题考查了函数的单调性、最值问题，考查导数的应用，是一道中档题．