
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 由b与cosB的值,利用余弦定理列出关系式,利用基本不等式变形求出ac的最大值,利用三角形的面积公式表示出三角形ABC的面积,将ac的最大值代入即可求出三角形ABC面积的最大值.
解答 解:∵b2=a2+c2-ac,即a2+c2-b2=ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,
∵B为三角形的内角,
∴B=$\frac{π}{3}$,sinB=$\frac{\sqrt{3}}{2}$,
∵b=2$\sqrt{3}$,cosB=$\frac{1}{2}$,
∴由余弦定理得:12=b2=a2+c2-ac≥ac,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{\sqrt{3}}{4}$ac≤3$\sqrt{3}$,
则△ABC面积的最大值为3$\sqrt{3}$.
故选:C.
点评 此题考查了余弦定理,三角形的面积公式,基本不等式的运用,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲水果生产的需要,该光源照射范围是∠ECF=$\frac{π}{6}$,点E,F的直径AB上,且∠ABC=$\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲水果生产的需要,该光源照射范围是∠ECF=$\frac{π}{6}$,点E,F的直径AB上,且∠ABC=$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
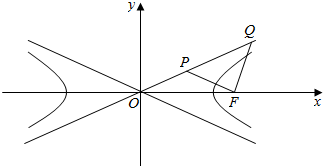
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com