
分析 (Ⅰ)法1:设直线m:x-2y+c=0与抛物线相切,则直线m与l的距离就是动点A到直线l:x-2y+13=0的最短距离,求出c=8,联立$\left\{{\begin{array}{l}{{y^2}=2px}\\{x-2y+c=0}\end{array}}\right.$,消x,利用△=16p2-8cp=0,即可求解抛物线C的方程为y2=8x
法2:设点A为$(\frac{a^2}{2p},a)$则点A到直线l:x-2y+13=0的距离d,通过d的最小值,求出2p=8,得到抛物线C的方程为y2=8x.
(Ⅱ)设过点B的切线方程为x-3=m(y-8),设$M(\frac{{{y_1}^2}}{8},{y_1}),N(\frac{{{y_2}^2}}{8},{y_2})$,则$\left\{{\begin{array}{l}{{y^2}=8x}\\{x-3=m(y-8)}\end{array}}\right.$,得到△=64m2-4(64m-24)=0,即2m2-8m+3=0,再利用△'=64-24=40>0,设两根为m1,m2,分别对应切线BM,BN,利用韦达定理,然后求解切点M坐标为$(2{m_1}^2,4{m_1})$,切点N坐标为$(2{m_2}^2,4{m_2})$,化简求解向量的数量积,推出结果.
解答 解:(Ⅰ)法1:由题意可知,设直线m:x-2y+c=0与抛物线相切,则直线m与l的距离就是动点A到直线l:x-2y+13=0的最短距离,即$\frac{|13-c|}{{\sqrt{5}}}=\sqrt{5}$,解得c=8或18
由图可知,抛物线C于直线l相离,故c<13,故c=8$\left\{{\begin{array}{l}{{y^2}=2px}\\{x-2y+c=0}\end{array}}\right.$,消x得y2-4py+2cp=0,则△=16p2-8cp=0,即c=2p
故2p=8,即抛物线C的方程为y2=8x
法2:设点A为$(\frac{a^2}{2p},a)$则点A到直线l:x-2y+13=0的距离$d=\frac{{|\frac{a^2}{2p}-2a+13|}}{{\sqrt{5}}}=\frac{{|\frac{1}{2p}{{(a-2p)}^2}-2p+13|}}{{\sqrt{5}}}$,由于a∈R,p>0,若-2p+13≤0,则d的最小值是0,不合题意,故-2p+13>0,且只有当a=2p时,d取到最小值$\frac{|-2p+13|}{{\sqrt{5}}}=\frac{-2p+13}{{\sqrt{5}}}=\sqrt{5}$,故2p=8,即抛物线C的方程为y2=8x
(Ⅱ)由题意可知,切线BM,BN的斜率存在且不等于0,设过点B的切线方程为x-3=m(y-8),设$M(\frac{{{y_1}^2}}{8},{y_1}),N(\frac{{{y_2}^2}}{8},{y_2})$,则$\left\{{\begin{array}{l}{{y^2}=8x}\\{x-3=m(y-8)}\end{array}}\right.$,得y2-8my+64m-24=0,△=64m2-4(64m-24)=0,即2m2-8m+3=0,由于其△'=64-24=40>0
不妨设两根为m1,m2,分别对应切线BM,BN,则${m_1}+{m_2}=4,{m_1}{m_2}=\frac{3}{2}$,
且由于y2-8my+64m-24=0具有等根,故y1=4m1,y2=4m2,
则切点M坐标为$(2{m_1}^2,4{m_1})$,切点N坐标为$(2{m_2}^2,4{m_2})$,
则$\overrightarrow{BM}•\overrightarrow{BN}=(2{m_1}^2-3,4{m_1}-8)(2{m_2}^2-3,4{m_2}-8)$=$4{({m_1}{m_2})^2}-6({m_1}^2+{m_2}^2)+9+16{m_1}{m_2}-32({m_1}+{m_2})+64$=$4{({m_1}{m_2})^2}-6[{({m_1}+{m_2})^2}-2{m_1}{m_2}]+9+16{m_1}{m_2}-32({m_1}+{m_2})+64$=$4{({m_1}{m_2})^2}-6[{({m_1}+{m_2})^2}-2{m_1}{m_2}]+9+16{m_1}{m_2}-32({m_1}+{m_2})+64=-100$.
点评 本题考查直线与抛物线的位置关系的综合应用,向量在解析几何中的应用,考查韦达定理以及判别式,直线与曲线相切的应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
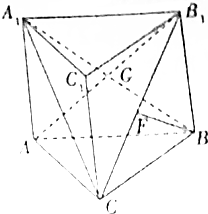 如图所示,在三棱柱ABC-A1B1C1中,矩形ABB1A1的对角线相交于点G,且侧面ABB1A1⊥平面ABC,AC=CB=BB1=2,F为CB1上的点,且BF⊥平面AB1C.
如图所示,在三棱柱ABC-A1B1C1中,矩形ABB1A1的对角线相交于点G,且侧面ABB1A1⊥平面ABC,AC=CB=BB1=2,F为CB1上的点,且BF⊥平面AB1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,0) | B. | (3,$\frac{π}{2}$) | C. | (-3,$\frac{2π}{3}$) | D. | (3,$\frac{11π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知AB,AC是圆的两条弦,过B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与AB相交于点E,AE=3,BE=1,则BC的长为( )
如图,已知AB,AC是圆的两条弦,过B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与AB相交于点E,AE=3,BE=1,则BC的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥V-ABC中,VA=VB=VC=2$\sqrt{3}$,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF分别交VB,VC于点E,F,求△AEF周长的最小值.
如图,在三棱锥V-ABC中,VA=VB=VC=2$\sqrt{3}$,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF分别交VB,VC于点E,F,求△AEF周长的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com