
分析 (1)将直线方程代入椭圆方程,根据直线由两个根,求得k的取值范围,根据韦达定理及直线方程求得x1+x2,x1•x2,y1y2和y1+y2,由斜率公式可知$\frac{{y}_{1}-1}{{x}_{1}}$•$\frac{{y}_{2}-1}{{x}_{2}}$=1,代入即可求得m的值,求得直线方程,即可证明直线l过定点M及点M的坐标;
(2)将m代入x1+x2和x1•x2,根据点到直线的距离公式、弦长公式及三角形的面积公式即可求得△BPQ面积表达式,设t=$\sqrt{{k}^{2}-4}$,代入根据基本不等式的关系即可求得△BPQ面积的最大值.
解答 证明:(1)直线AB的斜率存在,直线l的方程为y=kx+m,依题意得m≠±1,
设P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:(2k2+1)x2+4kmx+2(m2-1)=0,
△=16k2m2-4(2k2+1)(2m2-2)>0,
即2k2-m2+1>0,
x1+x2=-$\frac{4km}{2{k}^{2}+1}$,x1•x2=$\frac{2({m}^{2}-1)}{2{k}^{2}+1}$,
y1+y2=(kx1+m)+(kx2+m)=k(x1+x2)+2m=$\frac{2m}{1+2{k}^{2}}$,
y1•y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=$\frac{-2{k}^{2}+{m}^{2}}{1+2{k}^{2}}$,
∵k1k2=1
$\frac{{y}_{1}-1}{{x}_{1}}$•$\frac{{y}_{2}-1}{{x}_{2}}$=1,
y1y2-(y1+y2)-x1x2+1=0,
$\frac{-2{k}^{2}+{m}^{2}}{1+2{k}^{2}}$-$\frac{2m}{1+2{k}^{2}}$-$\frac{2({m}^{2}-1)}{2{k}^{2}+1}$+1=0,
即m2+2m-3=0,
解得:m=-3,m=1(舍去),
直线l:方程为y=kx-3,
故直线直线l过定点M,点M(0,-3);
解:(2)由(1)可知△=2k2-m2+1>0,即k2>4,
x1+x2=$\frac{12k}{2{k}^{2}+1}$,x1•x2=$\frac{16}{2{k}^{2}+1}$,
由弦长公式丨PQ丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,
=$\sqrt{1+{k}^{2}}$•$\frac{4\sqrt{{k}^{2}-4}}{2{k}^{2}+1}$,
=$\frac{4\sqrt{1+{k}^{2}}\sqrt{{k}^{2}-4}}{2{k}^{2}+1}$,
由点B(0,1)到直线y-kx+3=0的距离d=$\frac{丨1+3丨}{\sqrt{1+{k}^{2}}}$=$\frac{4}{\sqrt{1+{k}^{2}}}$,
∴△BPQ面积S=$\frac{1}{2}$•丨PQ丨•d=$\frac{8\sqrt{{k}^{2}-4}}{2{k}^{2}+1}$,
令t=$\sqrt{{k}^{2}-4}$,t>0,k2=t2+4,
S=$\frac{8t}{2{t}^{2}+9}$=$\frac{8}{2t+\frac{9}{t}}$≤$\frac{8}{6\sqrt{2}}$=$\frac{2\sqrt{2}}{3}$,
当且仅当2t=$\frac{9}{t}$,即t=$\frac{3\sqrt{2}}{2}$时,k=±$\frac{\sqrt{34}}{2}$时,取等号,
△BPQ面积的最大值$\frac{2\sqrt{2}}{3}$.
点评 本题考查直线与圆锥曲线的综合应用,考查根与系数的关系、弦长公式、点到直线的距离公式,考查学生分析问题解决问题的能力,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
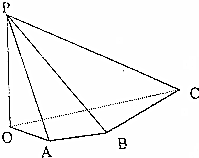 已知四棱锥P一OABC中,PO=3,OA=$\sqrt{7}$,AB=BC=4,PO⊥面OABC,PB⊥BC,且PB与平面OABC所成角为30°,求面APB与面CPB所成二面角的余弦值.
已知四棱锥P一OABC中,PO=3,OA=$\sqrt{7}$,AB=BC=4,PO⊥面OABC,PB⊥BC,且PB与平面OABC所成角为30°,求面APB与面CPB所成二面角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com