
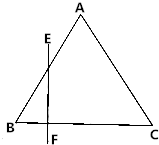
 如图,已知正三角形ABC的边长为6cm,当一条垂直于底边BC(垂足为F)的直线从左至右移动,与三角形有公共点时,直线把三角形分成两部分.设BF=x.
如图,已知正三角形ABC的边长为6cm,当一条垂直于底边BC(垂足为F)的直线从左至右移动,与三角形有公共点时,直线把三角形分成两部分.设BF=x.分析 (1)当0≤x≤3时,左侧图形为三角形,当3<x≤6时,左侧图形面积等于△ABC的面积减去右侧三角形的面积;
(2)分段做出函数的图象.
解答 解:(1)当0≤x≤3时,EF=$\sqrt{3}$BF=$\sqrt{3}x$,
∴y=S${\;}_{{\;}_{△BEF}}$=$\frac{1}{2}BF•EF$=$\frac{\sqrt{3}}{2}$x2.
当3<x≤6时,CF=6-x,∴EF=$\sqrt{3}CF$=$\sqrt{3}$(6-x),
∴y=S△ABC-S${\;}_{{\;}_{△CEF}}$=$\frac{1}{2}×6×6×\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$(6-x)2=-$\frac{\sqrt{3}}{2}$x2+6$\sqrt{3}$x-9$\sqrt{3}$.
∴y与x的函数关系式为:y=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}^{2},0≤x≤3}\\{-\frac{\sqrt{3}}{2}{x}^{2}+6\sqrt{3}x-9\sqrt{3},3<x≤6}\end{array}\right.$.
(2)作出函数的大致图象如下: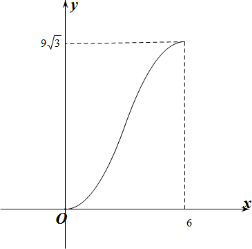
点评 本题考查了分段函数的图象,函数解析式的求解,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 332 | B. | -332 | C. | 320 | D. | -320 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示),将矩形折叠,使A点落在线段DC上,设折痕所在直线的斜率为k.
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示),将矩形折叠,使A点落在线段DC上,设折痕所在直线的斜率为k.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数也是偶函数 | B. | 偶函数 | ||
| C. | 既非奇函数也非偶函数 | D. | 奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-2,1) | C. | (-3,3) | D. | (-$\frac{5}{2}$,$\frac{3}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com