
 在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示),将矩形折叠,使A点落在线段DC上,设折痕所在直线的斜率为k.
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示),将矩形折叠,使A点落在线段DC上,设折痕所在直线的斜率为k.分析 (1)因为折叠过程中,A点落在线段DC上,特别的如果折叠后AD重合,这时候折痕所在直线的斜率为0,若AD不重合,这时候折痕所在直线的斜率不为0,然后根据A点和对折后的对应点关于直线折痕对称,我们可以求出直线方程.
(2)同(1)的分析,我们要对痕所在直线的斜率分类讨论,斜率为0时,易得结论,斜率不为0时,我们又要分折痕所在直线与矩形两边的交点在左右两边、上下两边、左下两边三种情况讨论,本小题分类情况比较多,故解答要细心!
解答 解:(1)
当k=0时,此时A点与D点重合,折痕所在的直线方程y=$\frac{1}{2}$.
当k≠0时,将矩形折叠后A点落在线段CD上的点为G(a,1)(0<a≤2),
所以A与G关于折痕所在的直线对称,有kOG•k=-1,即$\frac{1}{a}$•k=-1,∴a=-k.
故G点坐标为G(-k,1)(-2≤k<0).
从而折痕所在的直线与OG的交点坐标(线段OG的中点)为M(-$\frac{k}{2}$,$\frac{1}{2}$).
折痕所在的直线方程y-$\frac{1}{2}$=k(x+$\frac{k}{2}$),即y=kx+$\frac{{k}^{2}}{2}$+$\frac{1}{2}$(-2≤k<0).
由(1)、(2)得折痕所在的直线方程为:
k=0时,y=$\frac{1}{2}$;k≠0时y=kx+$\frac{{k}^{2}}{2}$+$\frac{1}{2}$(-2≤k<0).
(2)当k=0时,折痕的长为2.
当k≠0时,
①如下图,折痕所在的直线与边AD、BC的交点坐标为N(0,$\frac{{k}^{2}+1}{2}$),P(2,2k+$\frac{{k}^{2}+1}{2}$).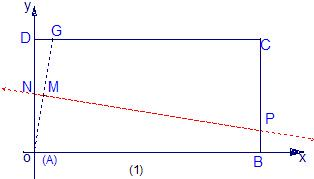
这时,-2+$\sqrt{3}$<k<0,y=PN2=4+4k2=4(1+k2)∈(4,16(2-$\sqrt{3}$)).
②如下图,折痕所在的直线与边AD、AB的交点坐标为N(0,$\frac{{k}^{2}+1}{2}$),P(-$\frac{{k}^{2}+1}{2k}$,0).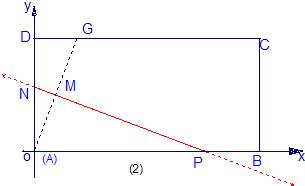
这时,-1≤k≤-2+$\sqrt{3}$,y=${(\frac{{k}^{2}+1}{2})}^{2}$+${(-\frac{{k}^{2}+1}{2k})}^{2}$.
y′=$\frac{{{(k}^{2}+1)}^{2}•({2k}^{2}-1)}{{2k}^{3}}$,令y′=0,可得k=-$\frac{\sqrt{2}}{2}$.
当x=-1时,y=2;
当x=-$\frac{\sqrt{2}}{2}$时,y=$\frac{27}{16}$;当x=-2+$\sqrt{3}$时,y=16(2-$\sqrt{3}$),
∴y∈[$\frac{27}{16}$,16(2-$\sqrt{3}$)]
③如下图,折痕所在的直线与边CD、AB的交点坐标为N($\frac{1{-k}^{2}}{2k}$,1),P(-$\frac{{k}^{2}+1}{2k}$,0).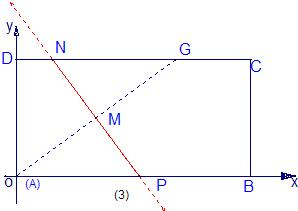
这时,-2≤k<-1,y=PN2=${(\frac{1}{k})}^{2}$+1∈[$\frac{5}{4}$,2).
综上述,ymax=16(2-$\sqrt{3}$),$\sqrt{16(2-\sqrt{3})}$,
所以折痕的长度的最大值为 $\sqrt{16(2-\sqrt{3})}$=2($\sqrt{6}$-$\sqrt{2}$).
点评 分类讨论思想是中学的四大数学思想之一,利用分类讨论思想一方面可将复杂的问题分解成若干个简单的问题,另一方面恰当的分类可避免丢值漏解,从而提高全面考虑问题的能力,提高周密严谨的数学教养.但在针对本题的解答中,要注意分析所有的可能情况,并要注意不重分,不漏分,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a5=$\frac{5}{9}$a2+$\frac{4}{9}$a9 | B. | a7=$\frac{7}{11}$a3+$\frac{4}{11}$a14 | C. | a6=$\frac{2}{3}$a5+$\frac{4}{3}$a8 | D. | a8=$\frac{2}{9}$a3+$\frac{7}{9}$a10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|2<x<3} | B. | {x|2<x≤4} | C. | {x|2<x≤4且x≠3} | D. | {x|-1<x≤6且x≠3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
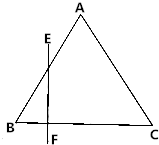 如图,已知正三角形ABC的边长为6cm,当一条垂直于底边BC(垂足为F)的直线从左至右移动,与三角形有公共点时,直线把三角形分成两部分.设BF=x.
如图,已知正三角形ABC的边长为6cm,当一条垂直于底边BC(垂足为F)的直线从左至右移动,与三角形有公共点时,直线把三角形分成两部分.设BF=x.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com