
分析 (Ⅰ)圆C:x2-4x+y2=0的圆心坐标为C(2,0),半径为2,CQ=sin30°×PC=$\frac{3}{2}<2$,由此能求出|MN|.
(Ⅱ)设直线l的方程为y=k(x+1),k≠0,联立$\left\{\begin{array}{l}{y=k(x+1)}\\{{x}^{2}-4x+{y}^{2}=0}\end{array}\right.$,得(1+k2)x2+(2k2-4)x+k2=0,由此利用根的判别式、韦达定理、向量的数量积能求出k的取值范围.
解答 解:(Ⅰ)圆C:x2-4x+y2=0的圆心坐标为C(2,0),半径为2,
∵P(-1,0),∴PC=3,
当直线l的倾斜角为30°时,过圆心C作直线l的垂线,垂足为Q,
在Rt△PQC中,sin30°=$\frac{CQ}{PC}$,∴CQ=sin30°×PC=$\frac{3}{2}<2$,
∴|MN|=2$\sqrt{4-(\frac{3}{2})^{2}}$=$\sqrt{7}$.
(Ⅱ)根据题意,直线l的斜率存在且不为0,
故可设直线l的方程为y=k(x+1),k≠0,
联立$\left\{\begin{array}{l}{y=k(x+1)}\\{{x}^{2}-4x+{y}^{2}=0}\end{array}\right.$,得(1+k2)x2+(2k2-4)x+k2=0,
设M(x1,y1),N(x2,y2),则△=(2k2-4)2-4(1+k2)k2>0,
解得$0<{k}^{2}<\frac{5}{4}$,
由韦达定理得${x}_{1}+{x}_{2}=\frac{4-2{k}^{2}}{1+{k}^{2}}$,${x}_{1}{x}_{2}=\frac{{k}^{2}}{1+{k}^{2}}$,
当∠MCN为钝角时,$\overrightarrow{CM}•\overrightarrow{CN}<0$,
∵$\overrightarrow{CM}$=(x1-2,y1),$\overrightarrow{CN}$=(x2-2,y2),
∴$\overrightarrow{CM}•\overrightarrow{CN}$=(x1-2,y2)•(x2-2,y2)
=x1x2-2(x1+x2)-4+y1y2
=$(1+{k}^{2}){{x}_{1}{x}_{2}+(k}^{2}-2)({x}_{1}+{x}_{2})+{k}^{2}+4$
=$(1+{k}^{2})•\frac{{k}^{2}}{1+{k}^{2}}$+(k2-2)•$\frac{4-2{k}^{2}}{1+{k}^{2}}$+k2+4
=$\frac{14{k}^{2}-4}{1+{k}^{2}}$,
由$\overrightarrow{CM}•\overrightarrow{CN}$<0,得14k2<4,
∴-$\frac{\sqrt{14}}{7}<k<\frac{\sqrt{14}}{7}$,k≠0,且满足0<k2<$\frac{4}{5}$,
∴k的取值范围是(-$\frac{\sqrt{14}}{7}$,0)∪(0,$\frac{\sqrt{14}}{7}$).
点评 本题考查线段长的求法,考查直线的斜率的取值范围的求法,是中档题,解题时要认真审题,注意圆的性质、根的判别式、韦达定理、向量的数量积的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
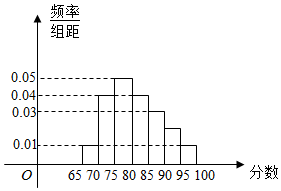 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的人数为19.
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的人数为19.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
| 对教师教学水平好评 | |||
| 对教师教学水平不满意 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100π}{3}$ | B. | 64π | C. | 100π | D. | $\frac{500π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{asinαsinβ}{sin(α-β)}$ | B. | $\frac{asinαsinβ}{cos(α-β)}$ | C. | $\frac{acosαcosβ}{sin(α-β)}$ | D. | $\frac{acosαcosβ}{cos(α-β)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com